标签:style blog http ar io os 使用 sp java
假设我们有一组房子面积和房价之间的关系的数据,并以面积作为横坐标,房价作为纵坐标把它画出来,有了这样的数据以后,假设给你一个房子的面积,要如何预测房子的价格呢?
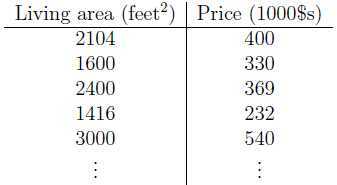
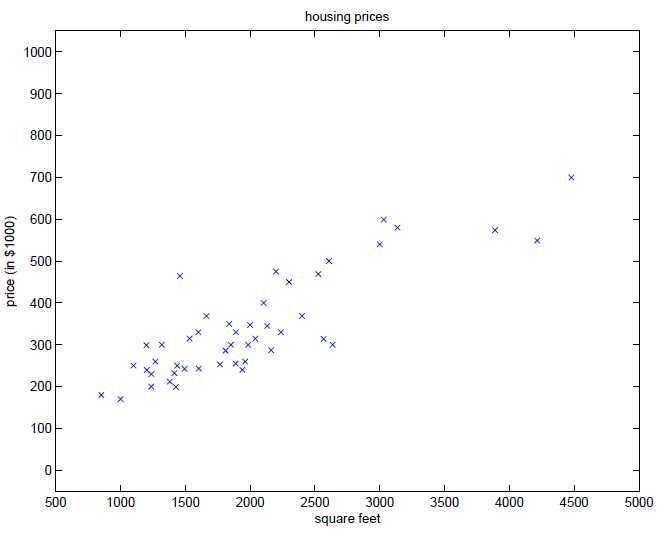
一种很直观的方法是使用训练数据拟合出一条直线出来,在线性回归里我们称为Hypothesis function,这里只有一个特征值(即房价),所以Hypothesis function为$$h_{\theta} (x)=\theta_{0} x_{0} + \theta_{1} x_{1}$$其中$x_{0}=1$,
当有多个特征值的时候Hypothesis function为:$$h_{theta} (x) = \sum_{i=0}^n \theta_i x_i = \theta^T x$$
那么现在给定一组训练数据,我们要如何选择$\theta$?
为了求解上述所说的选择$\theta$的问题,我们的做法就是使$h(x)$与$y$的值最相近,也就是说我们没组数据都会有一个预测值$h(x)$(通过Hypothesis function求解得到)以及真实值y,我们需要做的是使所有样本数据的预测值与真实值之间相差最小,因此定义如下代价函数:$$J(\theta) = \frac{1}{2} \sum_{i=1}^m (h_{\theta} (x^{(i)}) - y^{(i)})^2$$
这个代价函数实际上就是最小二乘法的回归模型。下面是一个特征值时候的描述:
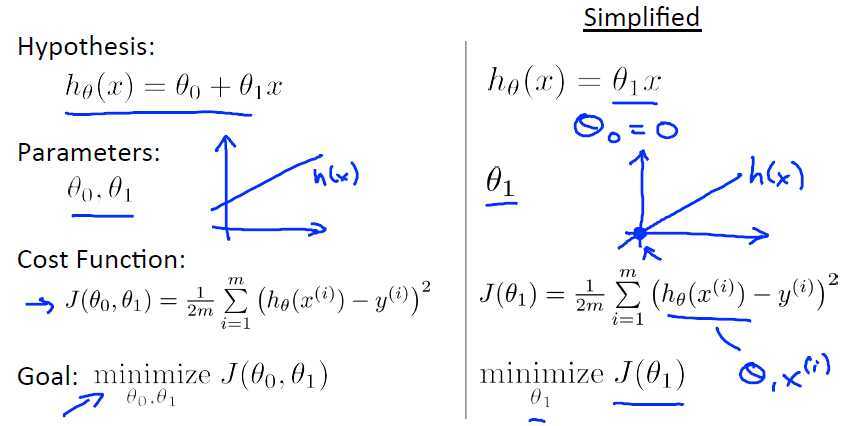
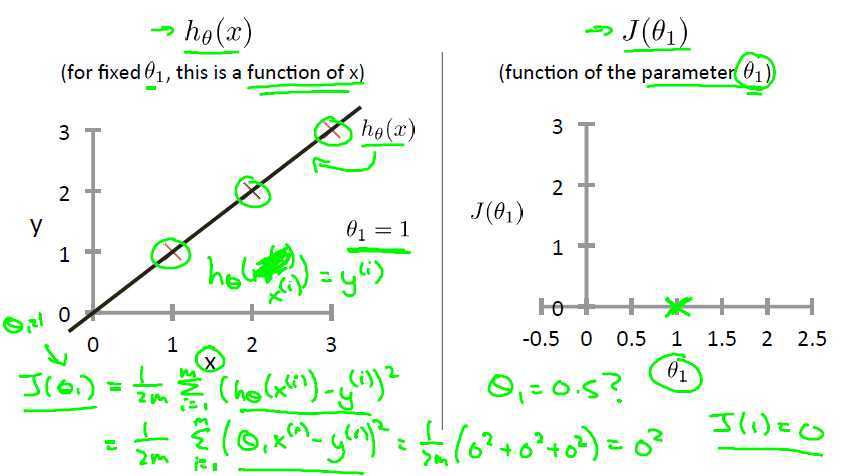
代价函数画出来的形式如下:
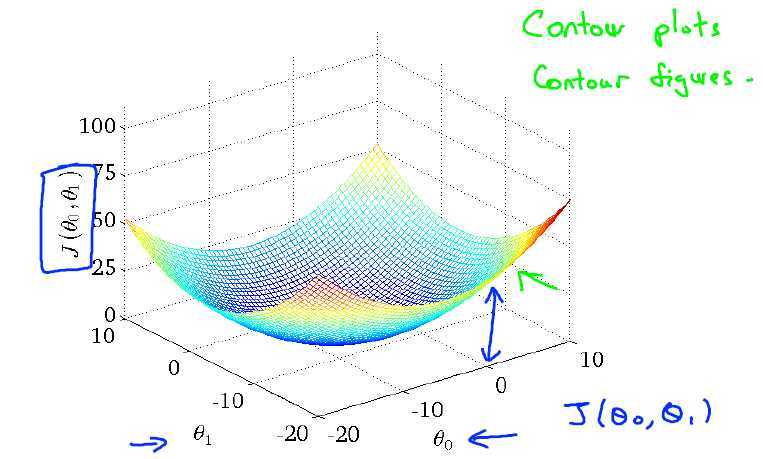
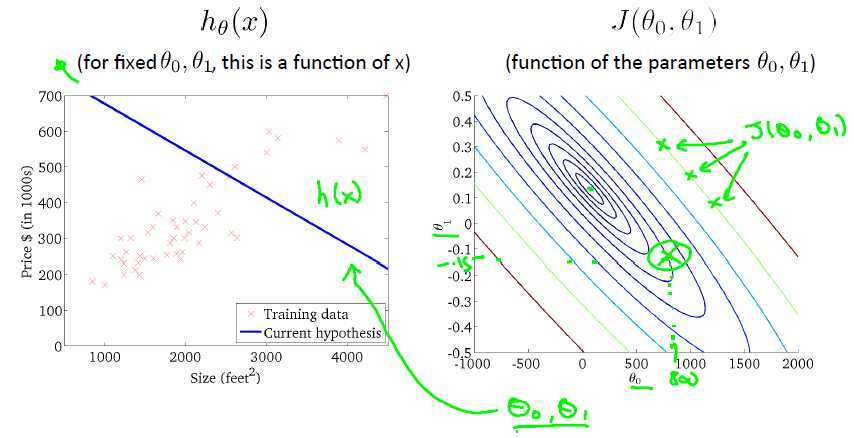
我们想要选择$\theta$来使的$J(\theta)$最小,这里我们使用梯度下降法来求解。$J(\theta)$是以$\theta$作为变量的函数,所以实际上就是对$\theta$求偏导,那么梯度实际上是一个由每一个变量的偏导组成的向量,向量的大小表示函数变化的值,向量的方向表示函数值下降最快的方向。
梯度下降法方法描述如下:
$\theta$每次更新的方法如下:$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta)$$
这里$\alpha$是学习率(Learning rate),为了实现这个算法,我们需要求$\frac{\partial}{\partial\theta_j}$:
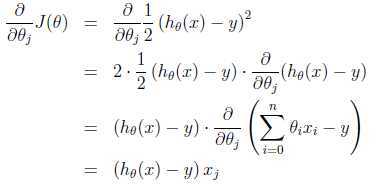
所以更新的法则如下所示:
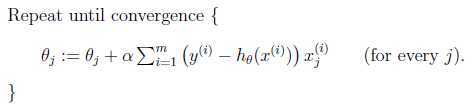
梯度下降的效果图形化效果:
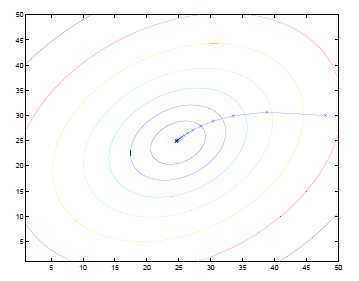
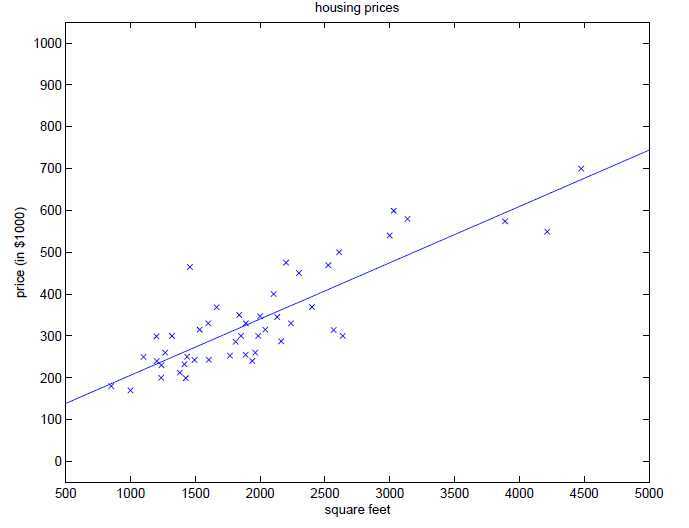
最后画出来的直线:
训练样本形式如下:
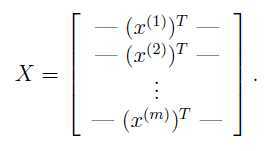
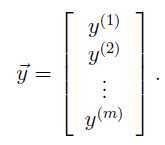
则:
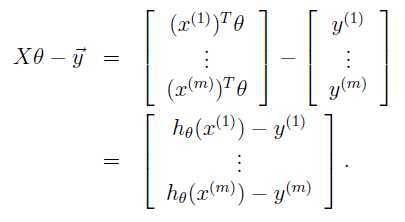
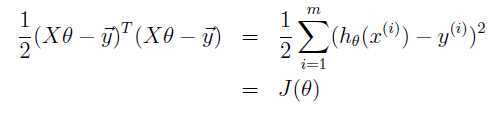
标签:style blog http ar io os 使用 sp java
原文地址:http://www.cnblogs.com/starlitnext/p/4172039.html