标签：

Cocos2d-x中的贝塞尔曲线

在Cocos2d-x中贝塞尔曲线运动的封装类为CCBezierTo和CCBezierBy。

这两个Action都需要传入一个参数ccBezierConfig，这是一个结构体，这个结构体有三个字段

1.CCPoint endPosition：结束点

2.CCPoint controlPoint_1：控制点1
3.CCPoint controlPoint_2：控制点2

两个控制点的会影响曲线的变化趋势。

Cocos2d-x中贝塞尔曲线运动的实现是二次曲线。

曲线的每个点的坐标是根据一个区间为0到1的变量t、开始点、结束点和两个控制点，通过方程计算出来的。

开始点就是精灵的当前位置，结束点和两个控制点通过ccBezierConfig这个结构体封装。

二次曲线

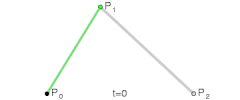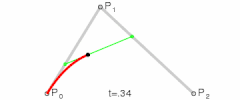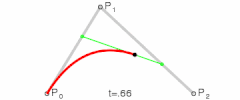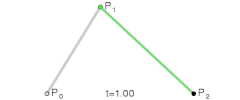
为建构二次贝塞尔曲线，可以中介点Q₀和Q₁作为由0至1的t：

• 由P₀至P₁的连续点Q₀，描述一条线性贝塞尔曲线。
• 由P₁至P₂的连续点Q₁，描述一条线性贝塞尔曲线。
• 由Q₀至Q₁的连续点B（t），描述一条二次贝塞尔曲线。

二次贝塞尔曲线的结构		二次贝塞尔曲线演示动画，t在[0,1]区间

controlPoint_1对应图中的点Q0

controlPoint_2对应图中的点Q1

>>点击查看贝塞尔曲线的更详细解释

实现

ParabolaTo.h

#ifndef __PARABOLATO_H__
#define __PARABOLATO_H__

#include "cocos2d.h"
USING_NS_CC;

// 抛物线运动
class ParabolaTo
{
public:
	/*创建一个抛物线动作
	参数：
		t					时间
		startPoint		开始点
		endPoint		结束点
		height			高度（影响抛物线的高度）
		angle			角度（贝塞尔曲线两个控制点与y轴的夹角，直接影响精灵的抛出角度）
	*/
	static CCEaseInOut* create(float t, CCPoint startPoint, CCPoint endPoint, float height = 0, float angle = 60);
};

#endif // !__PARABOLATO_H__

ParabolaTo.cpp

#include "ParabolaTo.h"

CCEaseInOut* ParabolaTo::create(float t, CCPoint startPoint, CCPoint endPoint, float height /* = 0 */, float angle /* = 60 */){

	// 把角度转换为弧度
	float radian = angle*3.14159/180.0;
	// 第一个控制点为抛物线左半弧的中点
	float q1x = startPoint.x+(endPoint.x - startPoint.x)/4.0;
	CCPoint q1 = ccp(q1x, height + startPoint.y+cos(radian)*q1x);		
	// 第二个控制点为整个抛物线的中点
	float q2x = startPoint.x + (endPoint.x - startPoint.x)/2.0;
	CCPoint q2 = ccp(q2x, height + startPoint.y+cos(radian)*q2x);
	
	//曲线配置
	ccBezierConfig cfg;
	cfg.controlPoint_1 = q1;
	cfg.controlPoint_2 = q2;
	cfg.endPosition = endPoint;
	//使用CCEaseInOut让曲线运动有一个由慢到快的变化，显得更自然
	return CCEaseInOut::create(CCBezierTo::create(t,cfg),0.5); 
}

调用示例：

	// 设置精灵的位置
	pBall->setPosition(ccp(50,50));	
	// 抛物线运动
	//pBall->runAction(ParabolaTo::create(1,pBall->getPosition(),ccp(450,50),100));
	// 加上旋转效果	
	pBall->runAction(
		CCSpawn::create(
			CCRotateBy::create(1,360),
			ParabolaTo::create(1,pBall->getPosition(),ccp(450,50),100)
			,NULL)
	);

以下是angle分别为60、30、80，height为100时，球的移动截图（图中的蓝点为两个控制点）。

angle是两个控制点连线与y轴之间的夹角，会直接影响球的抛出角度。

height会影响球移动时抛物线的高度

角度测量工具下载：http://pan.baidu.com/s/1c0zrnri

项目地址：https://coding.net/u/linchaolong/p/ParabolaAction/git

【Cocos2d-x】使用贝塞尔曲线（Bezier）实现精灵抛物线运动

标签：

原文地址：http://blog.csdn.net/linchaolong/article/details/42040667