标签:
本文主要介绍信息论中最基础但同时也是贯穿始终的四个概念,分别是信息熵、条件熵、互信息以及条件互信息。尝试着使用通俗易懂的语言,简单浅显的例子来使得大家对理解这几个数学概念提供一些帮助。
现在是信息爆炸的时代,我们都可以通过手机接入互联网,有可能你早上睁开眼睛的第一件事情就是刷个微博、看看新闻(虽然我很不赞同这么做^_^),我们接触到海量的各种消息,从当中我们获取信息,那么你有没有想过你到底得到了多少信息量呢?是不是我们看的新闻越多、读的材料越多就等同获取的信息量越多呢?虽然不排除它们之间存在一定的相关性,但是我相信很多人跟我一样,你阅读的这些消息如果不加以深入的思考的话,在你关上手机的时候这些平淡无奇的消息也随之在你的大脑中消失(- - !)。相反,如果某些小概率事件发生了,比如“马云,宣布到今年过年的时候给每一位淘宝用户发放1000元的红包”你在惊奇之余肯定不会忘了这件事情,除了猜想马云这样做的各种理由也给马云点赞!所以有理由相信,一个消息或者事件所能传递的信息的多少跟这件事情的发生概率有关系!那么现在要让你定义信息熵的数学表达式,你可能会用p(x)(x表示一个事件)来进行衡量,比如取个倒数,或者倒数的平方等等(因为p(x)是大于0小于1的)。然而香农这位数学家是利用的log(1/p(x)),这个表达式来进行度量的,至于他为什么这么做,我唯一能想到的就是为了之后数学推导上的便利(log可以把乘除法变成加减法),当然不排除香农老人家是为了让他的数学表达式看上去高大上一些(*_*)!!
那么信息熵的定义是不是到这里就结束了呢,很明显不是,虽然小概率事件的发生所能传递的信息量更多,但是它毕竟是小概率事件,发生的概率极低极低,所以在你的数学定义表达式当中必须有个因子来控制这种因素,最简单的做法就是直接相乘啦,用p(x) · log(1/(p(x)))来表示当前事件对整体信息熵的贡献值,香农他老人家也跟你的想法是一样的,信息论中信息熵的数学表达式:
$$H(x)=-\sum_{x}^{}p(x)log(p(x))$$
当log以2作为底时,信息量的单位就是bit。
到了这里,我们至少对什么是信息量,信息量为什么这么定义,这两个问题有了一定的认识,接下来举个例子对信息熵的应用做个简单的介绍!
试想离散均匀分布,其大小为N(表示每个事件发生的概率为1/N),那么你很容易套用上面的公式计算出这个随机变量所能传达的信息量为 log2(N) bits(这个结论还是蛮重要的)。从结果来看,好像是在说,离散均匀分布的size越大,其信息量越大。这个是不是能够很好的解释“世界之大,无奇不有”这句话呢!!
在定义了信息熵之后,信息论又引入了条件熵的概念,为什么这样呢?举个简单的例子。
比如我现在告诉你我在纸上准备写一个英文的单词,第一个字母我写下来是a,事实上以字母a作为开头的单词数以千计,现在你还不能猜到我想写什么单词,你或许可以翻下英文字典,发现以字母a开头的单词有1000个,假设各个英文单词服从均匀分布(事实上并非如此,因为有些常用词,有些生僻词),那么现在我写单词这个事情的信息量就是log(1000)bits(上文得出的结论)。那我接下来又写了一个字母p,你又接着查字典,发现以字母ap开头的单词一共有100个,那么现在这个事件的信息量只有log(100)bits,那我接下来又继续写单词,一直写到这个单词的前四个字母都出来了,appl,到了这个时候,你或许已经猜出来我想写的单词就是apple。所以我已经没有必要往下继续写啦。从这个例子可以看到,因为一定条件的发生,某个事情所能表示的信息量已经没有那么多了!到此,你应该明白了为什么要定义条件熵这个概念,那么我们到底怎么在数学上定义这个概念呢?很简单呀,如果要定义H(x|y)的话,参考H(x)的定义,把log(p(x))变成log(p(x|y))表示在y发生的条件下,x发生的概率。这个表示信息量的大小。再把p(x)变成p(x, y)表示x, y同时发生的概率,这个表示权值。再进行求和就可以得到最后的结果了。
$$H(x|y)=-\sum_{x,y}^{}p(x,y)log(p(x|y))$$
上面有提到,当一定条件下,某件事情所能表示的信息量已经没那么多了,事物之间的相互关联性导致了这种”不确定的减小“。那么,你现在也可以很清楚的知道$H(X)-H(X|Y)$这个数学表达式所代表的含义是什么了。没错,就是那些减小了的(消失不见)的“不确定性”。信息论中把这个叫做互信息,用$I(x;y)$来表示。它的数学上的定义是这样的:
$$I(X;Y)=\sum_{x,y}^{}p(x,y)log(\frac{p(x,y)}{p(x)p(y)})$$
关于它为什么这么定义,也很好解释,p(x,y)表示两者同时发生的概率,用来控制这个事件对信息量的贡献值,后面的$\frac{p(x,y)}{p(x)p(y)}$看似复杂,可以用条件概率公式把它换个形式$\frac{p(x|y)}{p(x)}$,它表示在$y$的条件下$x$继续发生的概率占原来概率$p(x)$的多少,以此来表示相关性,当$x$,$y¥相互独立时,$(x|y)=p(x)$,相除为$1$,计算值为$0$(表示不相关)。当$y$发生时$x$必然发生,那么$p(x|y)=1$,计算值就为$H(x)$,不确定性就完全消除了。
互信息这个物理量来表示事物之间的相关性到底是多大,它的应用范围可就大了。这里只阐述个自然语言处理领域的简单例子(参考这里[1])。
在自然语言处理中,经常要度量一些语言现象的相关性。比如在机器翻译中,最难的问题是词义的二义性(歧义性)问题。比如 Bush一词可以是美国总统的名字,也可以是灌木丛。那么如何正确地翻译这个词呢?具体的解决办法大致如下:首先从大量文本中找出和总统布什一起出现的互信息最大的一些词,比如总统、美国、国会、华盛顿等等,当然,再用同样的方法找出和灌木丛一起出现的互信息最大的词,比如土壤、植物、野生等等。有了这两组词,在翻译 Bush时,看看上下文中哪类相关的词多就可以了。
下面的一张图让你看懂信息熵与互信息之间的关系($H(x,y)$表示$X$,$Y$的联合熵,相对于$H(x)$只是增加了个变量而已):
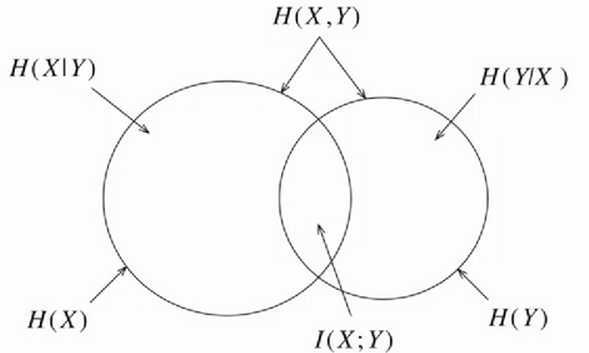
条件互信息表示在某个条件发生的情况下,事物之间的相关性还有多少,是变得更加相关呢?还是更加不相关呢?条件互信息的定义就是为了解决这个问题,它的定义与条件熵类似。
$$I(X;Y|Z)=\sum_{x,y,z}^{}p(X,Y,Z)log\frac{p(x,y|z)}{p(x|z)p(y|z)}$$
这个就不做过多的阐述了!
http://www.kuqin.com/math/20071204/2781.html
标签:
原文地址:http://www.cnblogs.com/Gru--/p/4176206.html