标签:
最短路径法:
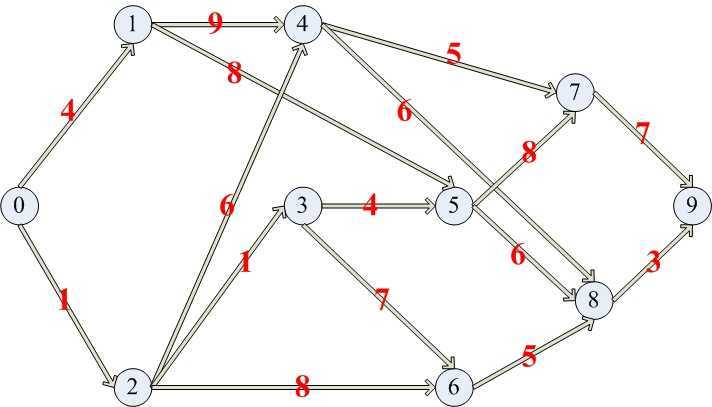
算法的主要思想是:单独一条边的路径也不一定是最佳路径。 从任意一条单边路径开始。所有两点之间的距离是边的权的和,(如果两点之间没有边相连, 则为无穷大)。 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。 先把所有的结果都计算出来放在数组里面,然后根据需要输出所需要的两点之间的最短路径。用了三个循环来实现
还有一个要Mark一下的是:不如一个数组s[i][j];那可以用这个数组来存放三个数 i,j和s[i][j];
Code:
#include<stdio.h> #include<stdlib.h> int a[100][100],cost=99999; int dian,bian,l,r;//点,边,要求距离的两个点 int main() { int i,j,k; printf("输入节点数和路径数\n"); scanf("%d%d",&dian,&bian); //初始化,将对角线全重置为0,其余的全部重置为99999 for(i=0;i<dian;i++) for(j=0;j<dian;j++) { if(i==j) a[i][j]=0; a[i][j]=99999; } //i和j表示节点;a[i][j]表示两点间距离 printf("输入节点i,j以及i,j之间的距离\n"); for(k=1;k<=bian;k++) { scanf("%d%d",&i,&j); scanf("%d",&(a[i][j])); } while(1) { printf("输入所求最短路径是哪两点\n"); scanf("%d%d",&l,&r);//输入所求最短路径是哪两点的距离; //核心算法程序:注意三个循环的顺序: int i,j,k; for(k=0;k<dian;k++) //固定一点k,三重循环 for(i=0;i<dian;i++) for(j=0;j<dian;j++) if(a[i][k]+a[k][j]<a[i][j]) a[i][j]=a[i][k]+a[k][j]; /* 若i到j的距离大于i到k再到j的距离, 那么i到j的距离的最小距离很自然变成了i到k再从k到j的距离, 随着k的变化再一步一步向后动态规划. */ printf("%d \n",a[l][r]); } return 0; } //Input sample: /* 10 16 0 1 4 0 2 1 1 4 9 1 5 8 2 4 6 2 3 1 2 6 8 3 5 4 3 6 7 6 8 5 4 7 5 4 8 6 5 7 8 5 8 6 7 9 7 8 9 3 Sample: 0 9 15 /*我自己写了一下,在把数组initializate的时候,那个循环条件是到点的数目,只有在输入几个边的距离的时候才是那个M*/
标签:
原文地址:http://www.cnblogs.com/tianjintou/p/4179189.html