华为机试—地铁换乘（图文吐血整理）

标签：华为机试   地铁换乘   最短路径   图   floyd   

题目：地铁换乘

描述：已知2条地铁线路，其中A为环线，B为东西向线路，线路都是双向的。经过的站点名分别如下，两条线交叉的换乘点用T1、T2表示。编写程序，任意输入两个站点名称，输出乘坐地铁最少需要经过的车站数量（含输入的起点和终点，换乘站点只计算一次）。
地铁线A（环线）经过车站：A1 A2 A3 A4 A5 A6 A7 A8 A9 T1 A10 A11 A12 A13 T2 A14 A15 A16 A17 A18
地铁线B（直线）经过车站：B1 B2 B3 B4 B5 T1 B6 B7 B8 B9 B1!0 T2 B11 B12 B13 B14 B15

输入：输入两个不同的站名

输出：所经过的站数及站的名称

基本思路：

其实分析问题就会发现，这是图论中的一个求最短路径的问题，是图算法的里面比较基础的。常见的求路径的有A星，Dijkstra算法,floyd算法等。

下面用floyd算法求解，三重循环简单暴力。

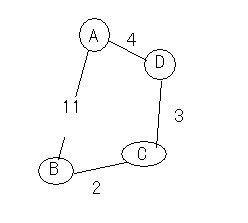
Floyd算法的基本思想如下：从任意节点A到任意节点B的最短路径不外乎2种可能：

1、是直接从A到B，

2、是从A经过若干个节点X到B。

所以，我们假设dis(AB)为节点A到节点B的最短路径的距离，对于每一个节点X，我们检查dis(AX) + dis(XB) < dis(AB)是否成立，如果成立，证明从A到X再到B的路径比A直接到B的路径短，我们便设置dis(AB)= dis(AX) +dis(XB)，这样一来，当我们遍历完所有节点X，dis(AB)中记录的便是A到B的最短路径的距离。

题目场景：

详细代码,带打印路径：

#include<iostream>  
#include<string>  
#include<stack>  
using namespace std;  
 
#define inf 1000  //定义无穷远距离   
#define stanum 35 //定义总站台数  
  
string staName[stanum] = {"A1","A2","A3","A4","A5","A6","A7","A8","A9","A10",  
                    "A11","A12","A13","A14","A15","A16","A17","A18",  
                    "B1","B2","B3","B4","B5","B6","B7","B8","B9","B10",  
                    "B11","B12","B13","B14","B15","T1","T2"} ; //记录车站的名字  
  

//floyd算法找出最短路径  
void floyd(int dis[][stanum],int path[][stanum])  
{  
    //初始化path矩阵  
    for(int row=0;row<stanum;row++)  
        for(int col=0;col<stanum;col++)  
            path[row][col]=row;  
  
    //找最短路径  
    for(int k=0;k<stanum;k++)  
        for(int i=0;i<stanum;i++)  
            for(int j=0;j<stanum;j++)  
                if(dis[i][j]>dis[i][k]+dis[k][j])  
                {  
                    dis[i][j]=dis[i][k]+dis[k][j];  
                    path[i][j]=path[k][j];  
                } 
				
}  
  
//转换车站的名字到矩阵的索引
int string2int(string s)  
{  
	for(int i=0;i<stanum;i++) { 
		if(s==staName[i])
		{  
			return i;  
            break;
		}  
	}
	return 0;
}  
  
void printres(int dis[][stanum],int path[][stanum],string start,string dest)  
{        
    int s;  
    int d; 
    s=string2int(start);  
    d=string2int(dest);  
    cout<<"最少经过的车站数量: "<<dis[s][d]+1<<endl; //输出站树加1包括了起始站  
  
	cout<<"经过的车站路径编号: ";
    for(int i=0;i<stanum;i++)  
        for(int j=0;j<stanum;j++)  
        {  
            if(i==s&&j==d) //输出路径  
            {  
                stack<int> pathrout;  //压栈  
                int k=j;  
                do{  
                    k=path[i][k];  
                    pathrout.push(k);  
  
                }while(k!=i);  
  
                //弹栈  
                cout<<staName[pathrout.top()];  
                pathrout.pop();  
                  
                int length=pathrout.size();  
                for(int t=0;t<length;t++)  
                {  
                    cout<<"->"<<staName[pathrout.top()];  
                    pathrout.pop();  
                      
                }  
                cout<<"->"<<staName[d]<<endl;  
				break;  
            }                  
        }   
}  
  
int main()  
{  
    int distance[stanum][stanum];  
    int path[stanum][stanum];  
    string start;  
    string dest;  
      
    //初始化连接矩阵  
    for(int i=0;i<stanum;i++)  
    {  
        for(int j=0;j<stanum;j++)  
        {  
            if(i==j)  
                distance[i][j]=0;  
            else  
                distance[i][j]=inf;  
        }  
    } 
	
    //初始化技巧  
    int sa[21]={0,1,2,3,4,5,6,7,8,33,9,10,11,12,34,13,14,15,16,17,0};  
    for(i=0;i<20;i++)  
    {  
        distance[sa[i]][sa[i+1]]=1;  
        distance[sa[i+1]][sa[i]]=1;  
    }  

    int sb[17]={18,19,20,21,22,33,23,24,25,26,27,34,28,29,30,31,32};  
    for(i=0;i<16;i++)  
    {  
        distance[sb[i]][sb[i+1]]=1;  
        distance[sb[i+1]][sb[i]]=1;  
    }  
  
  
    floyd(distance,path);
	
    cout<<"输入起点和终点: "<<endl;  
    
	while(cin>>start>>dest){
		printres(distance,path,start,dest); 
		printf("\n");
	}

    return 0;  
}  

华为机试—地铁换乘（图文吐血整理）

标签：华为机试   地铁换乘   最短路径   图   floyd   

原文地址：http://blog.csdn.net/wtyvhreal/article/details/42167249