标签:
目录
一、算法基本原理
1、图片预处理
2、找表盘
3、找指针
4、指针映射
5、求时间
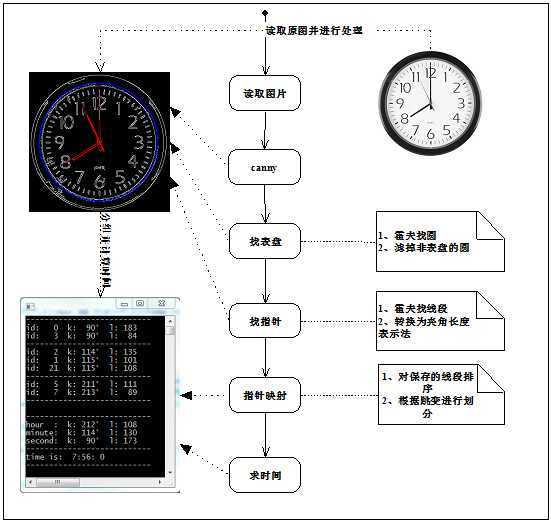
二、算法流程图
三、程序关键函数说明
1、Canny
2、HoughCircles
3、HoughLines2
4、MyLine类
5、平面几何相关函数
四、运行结果
五、实验中遇到的主要问题及解决方法:
1、在处理速度方面
2、去除其他圆的影响
3、霍夫找到的直线转换为夹角表示的线段
六、实验中的缺陷和不足
一、算法基本原理
时钟识别,顾名思义:就是根据一张带有钟表的图片识别出钟表上所展示的时间。对于这个问题我把它分为四步处理:
由于一张图片中包含的圆圈和直线的信息量较大,直接进行霍夫处理要浪费大量的运算量,而且也不利于去除各种干扰。于是这里所谓的预处理就是利用canny算法先对原图进行边缘提取,一方面滤掉部分干扰,另一方面将原图转换为边缘图后只剩下主要线条信息,有利于加快处理。实验证明,用此方法有用信息丢失较少,可以采用!
找表盘主要运用霍夫找圆,但是由于一张图里会找出很多圆,因此关键还是滤掉其他有影响的圆!这里采用的方法是找出所有用霍夫找到的圆中半径最大且整个圆都在当前图片中的那个圆作为表盘。实践证明,用这种方法能够较为准确的去除其他圆的影响并准确找到表盘所对应的圆(对了,这里的钟默认为圆形的表盘的指针式钟)。
找指针主要运用霍夫找线段,但是可想而知一张图里除了指针外一定还存在其他线段,而这些线段会对指针识别造成影响。因此我采用判断线段到圆心的距离小于一定的距离才默认为指针。然后对获取求得的线段进行转换为我定义的用斜率表示的线段的形式。
由于上面求得的线段并不是严格上的指针,而是很多线段,但是如果仔细观察会发现虽然并不是严格的对应关系,但是他们会出现成簇的分组效果!即:多条线段会聚集在某一个指针左右,而这些线段的斜率和预求得指针的斜率相差不大,我正是利用它的这个特点首先根据指针与X轴正方向的夹角从小到大进行排序,然后每次遇到相邻两个线段的夹角存在较大的跳变就进行切割,最后所有的线段被分割为一些组,再利用一个特殊的公式重新计算这组所代表指针的长度:
Le[num-1]=Le_ping[num-1]*0.2+Le_max[num-1]*0.8;
通过上面四步的计算我们已经能够将线段分为三组或者两组,这样再根据长短来和时分秒三个或者时分指针进行对应,再根据夹角就能求出对应的时间。
1、 Canny
void cvCanny( const CvArr* image,CvArr* edges,double threshold1,double threshold2, int aperture_size=3 );
说明: 开放计算机视觉(OpenCV)库库函数之一,用于对图像的边缘检测(采用canny算法)。
附加说明: 函数 cvCanny 采用 Canny 算法发现输入图像的边缘而且在输出图像中标识这些边缘。threshold1和threshold2 当中的小阈值用来控制边缘连接,大的阈值用来控制强边缘的初始分割。
2、 HoughCircles
CvSeq *cvHoughCircles(CvArr *image,void *circle_storage,int method,double dp,double min_dist,double param1,double param2,int min_radius,int max_radius);
说明:该函数用Hough变换在二值图像中中寻找圆,成功时返回CvSeq指针。
3、 HoughLines2
CvSeq* cvHoughLines2(CvArr* image,void* line_storage,int mehtod,double rho,double theta,int threshold,double param1 =0,double param2 =0);
说明: 此函数是opencv图像变换函数中的一个,主要用来访问霍夫变换的两个算法———标准霍夫变换(SHT)和累计概率霍夫变换(PPHT)。
CV_HOUGH_STANDARD - 传统或标准 Hough 变换. 每一个线段由两个浮点数 (ρ, θ) 表示,其中 ρ 是直线与原点 (0,0) 之间的距离,θ 线段与 x-轴之间的夹角。因此,矩阵类型必须是 CV_32FC2 type.
CV_HOUGH_PROBABILISTIC - 概率 Hough 变换(如果图像包含一些长的线性分割,则效率更高). 它返回线段分割而不是整个线段。每个分割用起点和终点来表示,所以矩阵(或创建的序列)类型是 CV_32SC4.
CV_HOUGH_MULTI_SCALE - 传统 Hough 变换的多尺度变种。线段的编码方式与 CV_HOUGH_STANDARD 的一致。
对传统 Hough 变换,不使用(0).
对概率 Hough 变换,它是最小线段长度.
对多尺度 Hough 变换,它是距离精度 rho 的分母 (大致的距离精度是 rho 而精确的应该是 rho / param1 ).
对传统 Hough 变换,不使用 (0).
对概率 Hough 变换,这个参数表示在同一条直线上进行碎线段连接的最大间隔值(gap), 即当同一条直线上的两条碎线段之间的间隔小于param2时,将其合二为一。
对多尺度 Hough 变换,它是角度精度 theta 的分母 (大致的角度精度是 theta 而精确的角度应该是 theta / param2).
4、 MyLine类
1 //----------------------------------------------------------------------------- 2 class MyLine{ 3 public: 4 int id;//编号 5 int k;//倾斜角[0-360) 6 int l;//长度 7 public: 8 MyLine(int ID=0,int K=0,int L=0){id=ID,k=K,l=L;}//构造函数 9 bool operator<(const MyLine &A){return k<A.k;}//重定义小于号 10 void print(){printf("id: %3d k: %3d° l: %3d\n",id,k,l);}//输出函数 11 };//自定义直线 12 //-----------------------------------------------------------------------------
5、 平面几何相关函数
1 //----------------------------------------------------------------------------- 2 //平面几何相关函数http://www.cnblogs.com/zjutlitao/p/3243883.html 3 //----------------------------------------------------------------------------- 4 #define eps 0.0000000001 5 #define PI acos(-1.0) 6 int dcmp(double x){ 7 if(fabs(x)<eps)return 0; 8 else return x<0 ? -1:1; 9 } 10 double Dot(Point A,Point B){return A.x*B.x+A.y*B.y;}//向量点积 11 double Length(Point A){return sqrt(Dot(A,A));}//向量模长 12 double Cross(Point A,Point B){return A.x*B.y-A.y*B.x;}//向量叉积 13 double Angle(Point A,Point B){return acos(Dot(A,B)/Length(A)/Length(B));}//求向量的夹角 14 double DistanceToLine(Point P,Point A,Point B)//点到直线的距离 15 { 16 Point v1=B-A,v2=P-A; 17 return fabs(Cross(v1,v2))/Length(v1);//如果不加绝对值是带有方向的距离 18 } 19 double DistancetoSegment(Point P,Point A,Point B){//点到线段的距离 20 if(A==B)return Length(P-A); 21 Point v1=B-A,v2=P-A,v3=P-B; 22 if(dcmp(Dot(v1,v2))<0)return Length(v2); 23 else if(dcmp(Dot(v1,v3))>0)return Length(v3); 24 else return fabs(Cross(v1,v2))/Length(v1); 25 } 26 //-----------------------------------------------------------------------------
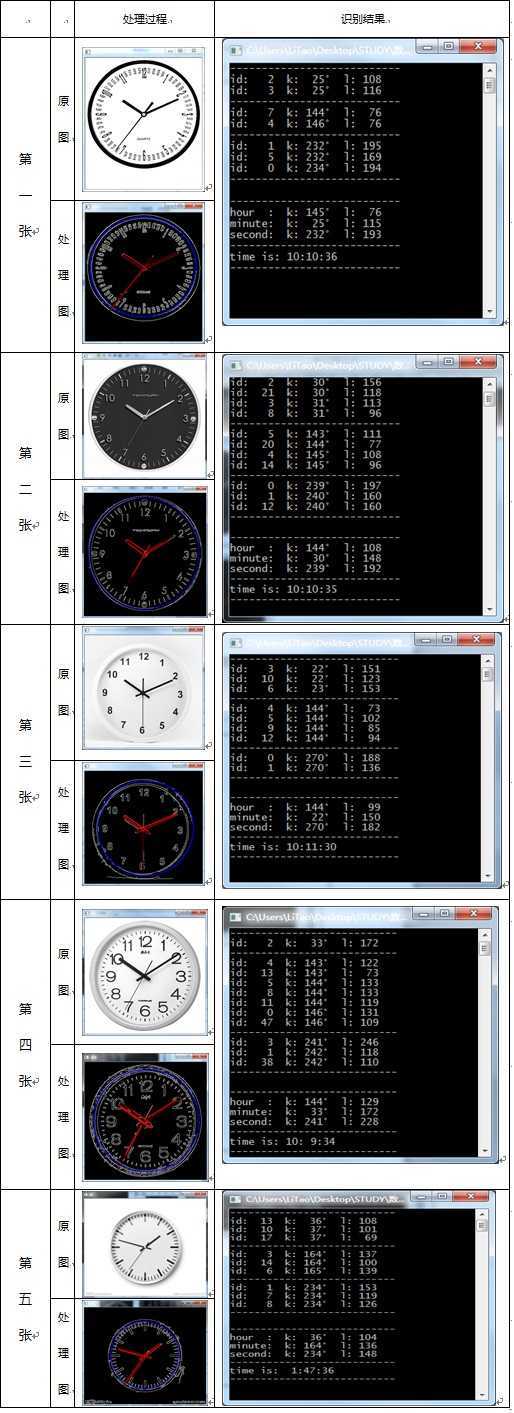
PS:由于篇幅有限,这里就不把全部的图片列出了~
1、在处理速度方面:
如果直接用原图做霍夫变换计算量巨大而且干扰特别多,这里我先用canny进行边缘提取预处理,然后再进行运算就解决了上述问题。但是用霍夫变换的图不能在上面绘制霍夫找到的直线或圆,结果就要转换为BGR彩图,才能进行可视化显示~具体的两个操作为:
- Canny(src, temp, 10, 140, 3);//提取边缘(如果不边缘提取就会浪费巨大时间)
- cvtColor(temp, dst, CV_GRAY2BGR);//将边缘提取的灰度图转换为BGR图便于画线
2、去除其他圆的影响:
由于用霍夫找圆会找到比较多的圆,如何在这些圆中找出和表盘最相近的一个呢?这里采用了比较巧妙的一个方法:
1 //储存检测圆的容器 2 std::vector<Vec3f> circles; 3 //调用Hough变换检测圆 4 //参数为:待检测图像,检测结果,检测方法(这个参数唯一),累加器的分辨率,两个圆间的距离,canny门限的上限(下限自动设为上限的一半),圆心所需要的最小的投票数,最大和最小半径 5 HoughCircles(temp,circles,CV_HOUGH_GRADIENT,2,50,200,100,100,300); 6 //找出圆盘(因为最大的不一定是的,所以加了几个限制条件) 7 int pos=0; 8 int max=-1; 9 for(size_t i = 0; i < circles.size(); i++ ) 10 { 11 Vec3f f=circles[i]; 12 if(f[2]>max && f[0]+f[2]<temp.rows && f[0]-f[2]>=0 && f[1]+f[2]<temp.cols && f[1]-f[2]>0) 13 { 14 max=f[2]; 15 pos=i; 16 } 17 } 18 Point center(circles[pos][0],circles[pos][1]);//找到的圆心 19 int radius= circles[pos][2];//找到的半径 20 circle(dst,center,radius,Scalar(255),2);
如上面所示:遍历所有霍夫找的圆,记录其中半径最大的且满足整个圆在图像内的那个,作为目标圆,这样就巧妙地找出了我们需要的那个圆~
3、霍夫找到的直线转换为夹角表示的线段:
因为接下来要根据夹角进行分组,所以这里要把霍夫找到的直线进行转换,这里我自己定义一个MyLine的类,用于保存一条线段,该线段形式为夹角和长度,其中转换关系为:
1 list<MyLine> list_MyLine; 2 vector<Vec4i> lines2;//线段检测 3 HoughLinesP(temp, lines2, 1, CV_PI/180, 50, 50, 10 ); 4 for( size_t i = 0; i < lines2.size(); i++ ) 5 { 6 Vec4i l = lines2[i]; 7 Point A(l[0], l[1]),B(l[2], l[3]); 8 if(DistancetoSegment(center,A,B)<30)//根据圆心到指针的距离阈值滤掉其他线段 9 { 10 bool down=(A.y+B.y-2*center.y>0);//判断长的在过圆心的水平线上部还是下部 11 if(A.x==B.x){//斜率为无穷的情况 12 list_MyLine.push_back(MyLine(i,90+(down?180:0),Length(Point(A.x-B.x,A.y-B.y)))); 13 }else if(A.y==B.y){//水平的情况 14 list_MyLine.push_back(MyLine(i,A.x+B.x-2*center.x>0 ? 0:180,Length(Point(A.x-B.x,A.y-B.y)))); 15 }else{ 16 if(down){ 17 if(A.y>center.y) 18 list_MyLine.push_back(MyLine(i,360-atan2(A.y-B.y,A.x-B.x)*180/PI,Length(Point(A.x-B.x,A.y-B.y)))); 19 else 20 list_MyLine.push_back(MyLine(i,360-atan2(B.y-A.y,B.x-A.x)*180/PI,Length(Point(A.x-B.x,A.y-B.y)))); 21 }else{ 22 if(A.y<center.y) 23 list_MyLine.push_back(MyLine(i,abs(atan2(A.y-B.y,A.x-B.x)*180/PI),Length(Point(A.x-B.x,A.y-B.y)))); 24 else 25 list_MyLine.push_back(MyLine(i,abs(atan2(B.y-A.y,B.x-A.x)*180/PI),Length(Point(A.x-B.x,A.y-B.y)))); 26 } 27 } 28 line(dst,A,B, Scalar(0,0,i*20+40), 2, CV_AA); 29 } 30 }
虽然用我这种识别方法可以快速有效的识别很多时钟,但是也存在一些特殊情况无法处理,比如:1、圆心不准导致计算出错;2、影子出现导致出现诡异指针;3、另类指针导致霍夫求得的直线不能准确描述指针;4、非圆形的表盘根本Hold不住;5、当存在其他干扰时表盘找不准;6、指针后半部分影响导致误判为另一个指针;7、指针长度检测错误导致时分秒针分配错误…等情况,虽然采用一些限制条件可以去除其中一二个错误,但是当算法向这方面偏的时候,又会导致另一些识别好的情况出现错误。最后总结一句:用图像识别不能求普遍性解决问题,我们应该根据具体的问题,在限定条件下进行研究,否则将永远满足不了需求!
链接:
本文链接:http://www.cnblogs.com/zjutlitao/p/4187476.html
文档下载:http://pan.baidu.com/s/1i3koenr
工程下载:http://pan.baidu.com/s/1jGst6lC
无法识别:http://pan.baidu.com/s/1o6t7rnG
更多精彩:http://www.cnblogs.com/zjutlitao/p/4125085.html
GitHub链接: https://github.com/beautifulzzzz/OpenCV-Clock-Identification
标签:
原文地址:http://www.cnblogs.com/zjutlitao/p/4187476.html