标签：

Josef和Andrew在2003年的ICCV上发表的论文[10]中，将文档检索的方法借鉴到了视频中的对象检测中。他们首先将图像的特征描述类比成单词，并建立了基于SIFT特征的vusual word dictionary，结合停止词、TF-IDF和余弦相似度等思想检索包含相同对象的图像帧，最后基于局部特征的匹配和空间一致性完成了对象的匹配。文档检索与计算机视觉之间渊源颇深，在CV领域常常会遇到要将图像的多个局部特征描述融合为一条特征向量的问题，比如常用的BoVW、VLAD和Fisher Vector等。下面，我们从文档检索为切入点，简单学习下这些局部特的融合方法。

Document Retrieval

文档检索系统中一般包含几个标志的步骤：

1. 将整个文档分割成单词.英文文档的分词很容易完成，因为各单词间都是由空格隔开的，但是中文分词本身就是个颇有技术含量的事情了。目前比较好的中文分词项目有ICTCLAS，Paoding，FudanNLP，IKAnalyzer和Jieba等。
2. 将每个单词用其词根表示(中文不需要此步骤）。比如walk,walking和walks都用walk表示。
3. 利用停用词(stop word)表过滤最常见的单词，比如”的“、”啊“等。不过有些情况下，我们需要的也许正好是这些停用词表中的单词，所以现在有些系统中其实也保留了一部分停用词的。
4. 剩下的单词组成整个语料库的词典，每个单词有一个用于标识的ID。对于超大的语料库，词典包含的单词数目至少也是百万级别的，所以也需要哈希标或树等高效的数据结构来组建词典，以加快搜索时的查询速度。
5. 每个文档用一个向量\(F=\{f_1,\cdots,f_K\}\)表示，其中向量的每个维度表是该维度对应的单词在文档中出现的次数。由于该向量很稀疏，所以可以用稀疏向量的形式存储，即用(word id,fequency)的形式存储每个非零元素即可。
6. 建立倒排索引(inverted index)，如图1所示。
7. 为向量的每个维度计算权重形成新的向量\(V=\{w_1,\cdots,w_K\}\): \begin{equation} w_i=\frac{f_i}{f}\log\frac{N}{n_i} \end{equation} 其中\(f_i\)为第\(i\)个单词在文档中出现的次数;\(f\)为文档经过过滤后的总单词数;\(N\)为整个语料库的文档数目;\(n_i\)为包含第\(i\)个单词的文档数目。TFIDF背后的思想也很直白：在一个文档中出现次数最多的单词更可能是该文档的主要关键词;如果该单词在很多文档中都出现，那么该单词其实并无很丰富的信息量。
8. 根据查询关键词，从倒排索引中取出包含关键词的文档的向量，然后与查询关键词组成的向量直接计算余弦相似度，最后结合相似读和文档自身的权重进行排序后返回给用户。

Bag of Visual Words

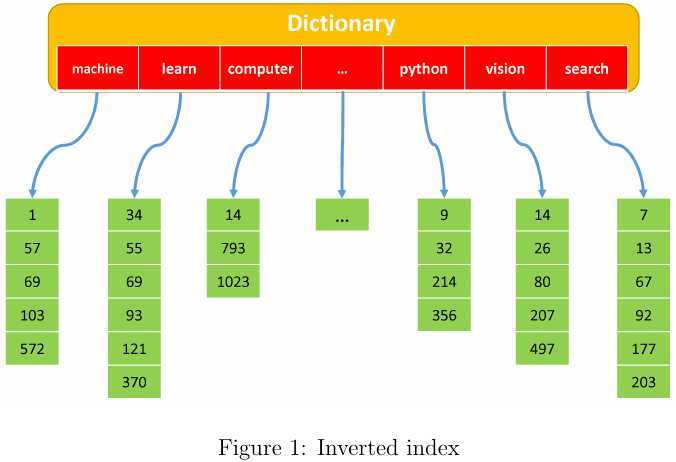
大规模图像检索不仅要考虑检索的正确率,也要考虑时间和空间的开销.目前最流行的图像特征表示方法莫过于bag of viusal words(BoVW),该方法借鉴了自然语言处理(Natural Language Processing,NLP)中的词袋思想,如图2所示. BoVW的处理流程如图3所示,其过程描述如下:

1. 在图像集上提取SIFT等特征描述子\(\{d_i\in\mathbb{R}^n|i=1,\cdots,N\}\);
2. 基于这些特征描述子用KMeans或GMM进行聚类分析,得到的聚类中心\(\{c_k\in\mathbb{R}^n|k=1,\cdots,K\}\)即为viusal dictionary中的每一个visual word,到此词典的建立完成;
3. 提取图像的特征描述子\(\{d_j\in\mathbb{R}^n|j=1,\cdots,m\}\),用hard或soft的量化方法[11]计算特征描述子落到每个visual word的概率\(\gamma_j=[\gamma_{j1},\cdots,\gamma_{jK}]\),并用\(\sum_{j=1}^m\gamma_j\)构成的直方图表示每一张图片。
4. 最后的BoVW向量还需要进一步用\(L_2\)范式归一化,然后用IDF(inverse document frequency)的思想为每个visual word分配权重。

那么基于BoVW,我们怎么来进行图像搜索?是否能从网页搜索中获得些许灵感呢?搜索引擎常用的倒排索引在这里也可以有用武之地。

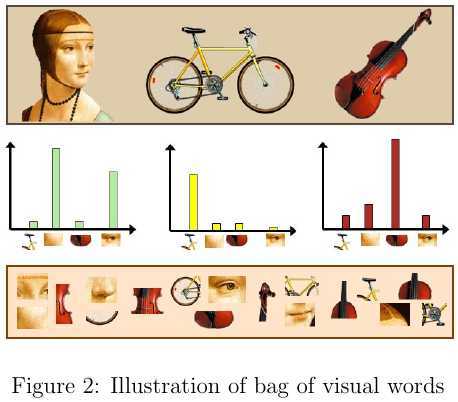
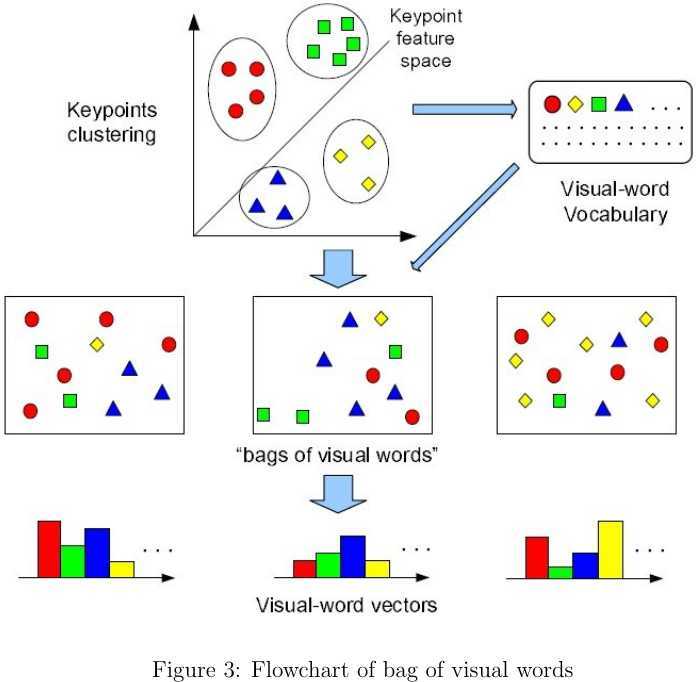
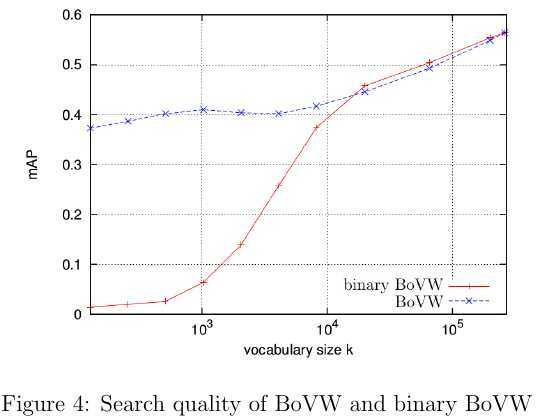
BoVW的成功主要是源于两点:1)诸如SIFT等强大的局部特征描述子[7,12,13]为BoVW奠定了坚实的基础;2)用BoVW形式得到的特征描述是与词典(visual dictionary)容量等长的向量,很容易用欧式距离或余弦距离等度量准则计算两个样本之间的相似度,继而可以运用SVM或LR等成熟的分类或回归算法完成后续任务. 但是在大规模图像搜索中,基于BoVW的特征向量的维度通常会高达上百万.为了降低存储开销,有学者提出了将BoVW进一步压缩成二进制[4,10],即抛弃每个visual word出现的频度,仅用1或0表示出现或者未出现.如此一来,存储开销变成了原来的八分之一,但是准确度也比原始的BoVW低一些.据论文[4]中的实验结果,二进制形式的BoVW在visual dictionary的维度高达30,000的时候准确度才和原始BoVW特征的相当,如图4所示.其实高维向量通常都很稀疏,另一个降低存储开销的策略就是用(位置,值)之类的二元组存储非零元素;对于二进制的BoVW,仅存储位置信息即可.此外,若采用[10]中的倒排列表(inverted lists)会大大加快检索速度. 

Vector of Locally Aggregated Descriptors

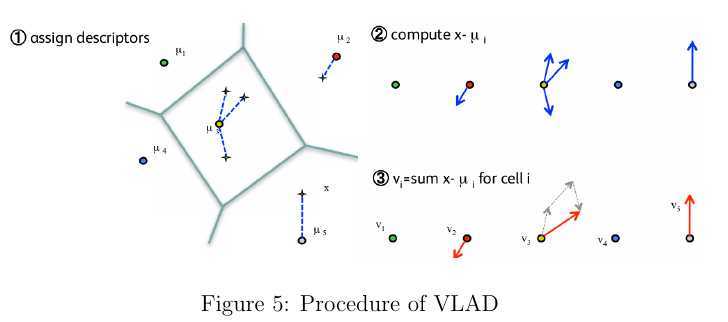
VLAD(vector of locally aggregated descriptors)[5]聚合了SIFT等局部特征后产生一种紧凑的特征描述,其计算复杂性/存储开销和有效性方面都介于BoVW和Fisher Vector[9]之间.VLAD构建词典\(\mathcal{C}=\{c_1,\cdots,c_k\}\)的过程与BoVW类似，只不过最后累加了分配到\(c_i\)的所有样本与\(c_i\)的差值\(x-c_i\)。VLAD可被视为Fisher Vector的简化版本，描述了各特征向量相对于visual word更丰富的一阶统计信息。假设局部特征描述子的维度为\(d\)，那么VLAD的特征维度\(D=k\times d\)，其中与每个visual word相关联的特征向量 \begin{equation} v_i=\sum_{\text{x such that }NN(x)=c_i}x-c_i \end{equation} 这些残差叠加的结果即为最后如图5所示的VLAD特征描述： \begin{equation} V=\begin{bmatrix} v_1\\ \vdots\\ v_k \end{bmatrix}\in\mathbb{R}^{k\times d} \end{equation} 最后，需要对得到的VLAD向量进行归一化处理，最常见的归一化方就是针对每个\(v_i\)除以其对应的\(L_2\)范数[2]，或者对\(V\)中的每个元素\(z\)执行变换\(sign(z)\sqrt{z}\)，然后在此基础上用全局的\(L_2\)范数进行归一化处理。 根据实验结果，即使在visual word数目相对较小的前提下\(k\in[16,256]\)仍能获得比较出色的效果。 

Fisher Vector

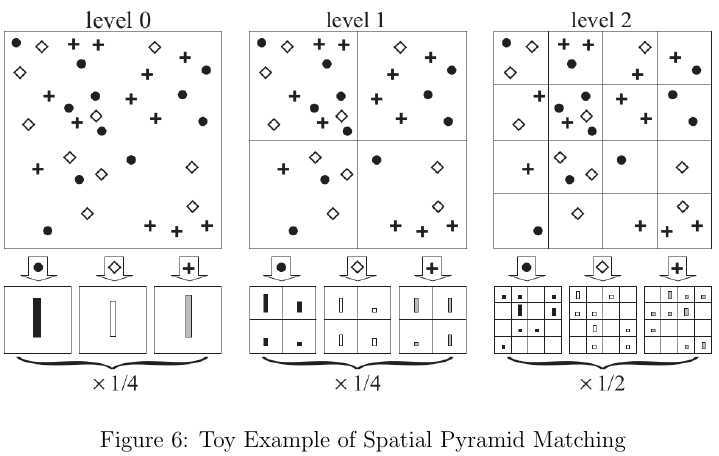
在图像分类和检索等应用中，基于BoVW集成的特征表述通常存在稀疏和高维度的问题。用FV(Fisher Vector)特征向量可以获得更为紧凑的特征描述，更适用于图像分类和检索等问题。FV可以作为Fisher Kernel[3]的一种特例推导出来。Fisher Kernel作为一种核函数，其作用也是计算两个样本间的相似程度。与多项式核函数、RBF核函数等普通核函数不同的是，Fisher Kernel计算的是样本\(x\)与\(x‘\)在产生式模型\(p(x|\Theta)\)中相似度。模型参数\(\Theta\)通常是基于一批训练样本通过最大似然参数估计的方法得到的，使得假定的概率模型能最大限度拟合数据的先验分部情况。在学习到概率模型\(p(x|\Theta)\)后，每个样本在核空间的表述形式如下： \begin{equation} \hat{\Phi}(x)=\nabla_{\Theta}\log p(x|\Theta) \end{equation} 其中\(\hat{\Phi}(x)\)可视为该样本对模型参数的影响程度。接下来还需要对\(\hat{\Phi}(x)\)进行白化变换(Whitening Transform)[1]，使其变换为白化向量(白化向量的每个维度服从均值为零、方差有限的概率分布)，且对应的协方差矩阵为单位阵，其目的是进一步消除各维度间的相关性，减小数据的冗余度。由于模型参数\(\Theta\)是用最大似然估计得到的，\(\hat{\Phi}(x)\)为对数似然函数的梯度，因此有\(E[\hat\Phi(x)]=0\)。因为\(\hat{\Phi(x)}\)已经经过了中心化处理，其协方差矩阵如下： \begin{equation} H = E_{x \sim p(x|\Theta)} [\hat\Phi(x) \hat\Phi(x)^T] \end{equation} 最终的FV编码\(\Phi(x)\)由经过白化变换的对数似然函数的梯度给出： \begin{equation} \Phi(x) = H^{-\frac{1}{2}} \nabla_\Theta \log p(x|\Theta). \end{equation} 最终，经过Fisher Kernel计算样本间相似度的形式为： \begin{equation} K(x,x‘) = \langle\Phi(x),\Phi(x‘) \rangle = \nabla_\Theta \log p(x|\Theta)^\top H^{-1} \nabla_\Theta \log p(x‘|\Theta) \end{equation} Fisher Vector的设计初衷在于将图像的局部特征描述编码成便于学习和度量的向量。我们假定\(D\)维的局部特征\(\{x_1,\cdots,x_n\}\)由\(K\)个混合的高斯模型(Gaussian Mixture Model,GMM)生成，其中GMM的参数为\(\Theta=(\mu_k,\Sigma_k,\phi_k;k=1,\cdots,K)\)。为了简化高斯混合模型，假设\(\Sigma_k=\sigma_k^2,\sigma_k\in\mathbb{R}^D_+\)。生成局部特征描述的产生式模型由混合高斯模型的密度函数给出： \begin{equation} p(x|\Theta)=\sum_{k=1}^K\pi_kp(x|\Theta_k) \end{equation} 其中，\(\Theta_k=(\mu_k,\Sigma_k)\)，并且 \begin{equation} \begin{split} p(x|\Theta_k)&=\frac{1}{(2\pi^{\frac{D}{2}})\sqrt{|\Sigma_k|}}\exp\left[-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)\right]\\ &=\frac{1}{(2\pi^{\frac{D}{2}})\sqrt{\sigma^2_k}}\exp\left[-\frac{(x-\mu_k)^T(x-\mu_k)}{2\sigma_k^2}\right] \end{split} \end{equation} Fisher Vector需要计算对数似然函数对各模型参数的倒数，下面仅考虑特定模式的参数\(\Theta_k\)。由于高斯密度函数中含有指数函数，其梯度可以写成如下形式： \begin{equation} \nabla_{\Theta_k} p(x|\Theta_k) = p(x|\Theta_k) g(x|\Theta_k) \end{equation} 那么对数似然函数的倒数形式如下： \begin{equation} \nabla_{\Theta_k} \log p(x|\Theta) = \frac{\pi_k p(x|\Theta_k)}{\sum_{t=1}^K \pi_k p(x|\Theta_k)} g(x|\Theta_k) = q_k(x) g(x|\Theta_k) \end{equation} 其中\(q_k(x)\)是用软分配的形式表示样本\(x\)分配到第\(k\)个模式的概率。根据论文[8]的方法，我们进行近似处理：如果\(x\)采样自地\(k\)个模式，那么\(q_k(x)\approx 1\)，否则\(q_k(x)\approx 0\)，因此得到下式： \begin{equation} \begin{split} &E_{x \sim p(x|\Theta)} [ \nabla_{\Theta_k} \log p(x|\Theta) \nabla_{\Theta_t} \log p(x|\Theta)^T ]\\ \approx &\begin{cases} \pi_k E_{x \sim p(x|\Theta_k)} [g(x|\Theta_k) g(x|\Theta_k)^T], & t = k, \\ 0, & t\not=k. \end{cases} \end{split} \end{equation} 在该近似计算的基础上，各高斯模型的参数之间已经不存在任何相关性了。接下来，计算\(g(x|\Theta_k\): \begin{equation} g(x|\Theta_k) = \begin{bmatrix} g(x|\mu_k) \\ g(x|\sigma_k) \end{bmatrix} \end{equation} 其中 \begin{equation} [g(x|\mu_k)]_j = \frac{x_j - \mu_{jk}}{\sigma_{jk}^2} \end{equation} \begin{equation} [g(x|\sigma_k^2)]_j = \frac{1}{2\sigma_{jk}^2} \left( \left(\frac{x_j - \mu_{jk}}{\sigma_{jk}}\right)^2 - 1 \right) \end{equation} 那么模型的协方差如下： \begin{equation} \begin{split} H_{\mu_{jk}} &= \pi_k E[g(x|\mu_{jk})g(x|\mu_{jk})] \\ &=\frac{\pi_k}{\sigma_{jk}^2}\int\left(\frac{x_j-\mu_{jk}}{\sigma_{jk}}\right)^2p(x|\Theta_k)dx_{j}\\ &=\frac{\pi_k}{\sigma_{jk}^2}\int \frac{-t^2}{\sqrt{2\pi}}e^{\frac{t^2}{2}}dt\\ &=\frac{\pi_k}{\sigma_{jk}^2\sqrt{2\pi}}\left[\left.-te^{-\frac{t^2}{2}}\right|^{+\infty}_{-\infty}+\int e^{-\frac{t^2}{2}}dt\right]\\ &= \frac{\pi_k}{\sigma_{jk}^2} \end{split} \end{equation} 同理，可得 \begin{equation} H_{\sigma_{jk}^2} = \frac{\pi_k}{2 \sigma_{jk}^4} \end{equation} 那么，对于图像的一个特征描述\(x\)得到的FV编码形式为： \begin{equation} \Phi_{\mu_{jk}}(x) = H_{\mu_{jk}}^{-\frac{1}{2}} q_k(x) g(x|\mu_{jk}) = q_k(x) \frac{x_j - \mu_{jk}}{\sqrt{\pi_k}\sigma_{jk}} \end{equation} \begin{equation} \Phi_{\sigma^2_{jk}}(x) = H_{\sigma^2_{jk}}^{-\frac{1}{2}}q_k(x)g(x|\sigma^2_{jk})=\frac{q_k(x)}{\sqrt{2 \pi_k}} \left[\left(\frac{x_j - \mu_{jk}}{\sigma_{jk}}\right)^2 - 1 \right] \end{equation} 据论文[9]的研究表明，先验概率参数\(\pi_k\)对特征描述的贡献较小，因此在这里就被忽略了。假设生成的所有局部特征描述都是服从独立同分布的，那么对于一副图形的\(N\)个特征描述\(\{x_1,\cdots,x_N\}\)，其整体的FV编码形式如下： \begin{equation} \begin{split} u_{jk} &= {1 \over {N \sqrt{\pi_k}}} \sum_{i=1}^{N} q_{ik} \frac{x_{ji} - \mu_{jk}}{\sigma_{jk}}, \\ v_{jk} &= {1 \over {N \sqrt{2 \pi_k}}} \sum_{i=1}^{N} q_{ik} \left[ \left(\frac{x_{ji} - \mu_{jk}}{\sigma_{jk}}\right)^2 - 1 \right] \end{split} \end{equation} 其中\(j=1,\cdots,N\)表示特征向量的每个维度。每个图像\(I\)的整体特征描述可由\(\mathbf{u}_k\)和\(\mathbf{v}_k\)叠加成的向量表示： \begin{equation} \Phi(I) = \begin{bmatrix} \vdots \\ \mathbf{u}_k \\ \vdots \\ \mathbf{v}_k \\ \vdots \end{bmatrix} \end{equation} 为了进一步提升Fisher Vector的性能，还需要归一化，常用的包括L2-norm、Power-norm。此外，还可以结合空间金字塔匹配(Spatial Pyramid Matching)[6]，其基本思想是将图像分割成若干大小不等的窗口，然后计算各窗口的特征直方图并用池化(Pooling)组合，最后将不同粒度下的特征加权组合成为最终的特征描述，如图6所示。

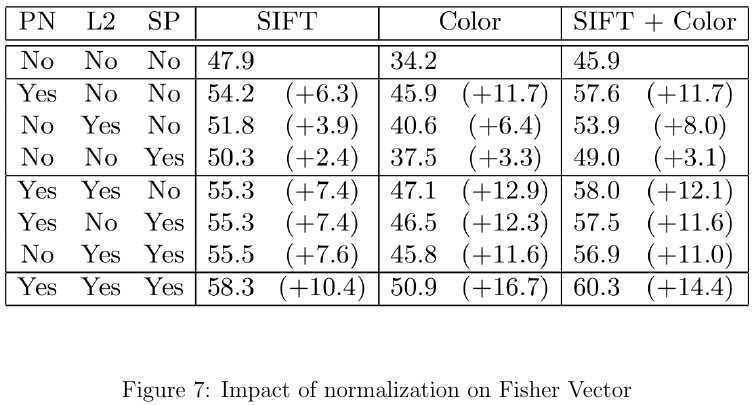
据论文[9]的实验，结合了L2-norm、Power-norm和金字塔匹配，其结果对比如图7所示。 

References

• [1] Whitening transformationn. http://en.wikipedia.org/wiki/Whitening_transformation.
• [2] Relja Arandjelovic and Andrew Zisserman. All about vlad. In Computer Vision and Pattern Recognition (CVPR), 2013 IEEE Conference on, pages 1578–1585. IEEE, 2013.
• [3] Tommi Jaakkola, David Haussler, et al. Exploiting generative models in discriminative classifiers. Advances in neural information processing systems, pages 487–493, 1999.
• [4] Herv ?e J ?egou, Matthijs Douze, and Cordelia Schmid. Packing bag-of-features. In Computer Vision, 2009 IEEE 12th International Conference on, pages 2357–2364. IEEE, 2009.
• [5] Herv ?e J ?egou, Matthijs Douze, Cordelia Schmid, and Patrick P ?erez. Aggregating local descriptors into a compact image representation. In Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pages 3304–3311. IEEE, 2010.
• [6] Svetlana Lazebnik, Cordelia Schmid, and Jean Ponce. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on, volume 2, pages 2169–2178. IEEE, 2006.
• [7] David G Lowe. Distinctive image features from scale-invariant keypoints. International journal of computer vision, 60(2):91–110, 2004.
• [8] Florent Perronnin and Christopher Dance. Fisher kernels on visual vocabularies for image categorization. In Computer Vision and Pattern Recognition, 2007. CVPR’07. IEEE Conference on, pages 1–8. IEEE, 2007.
• [9] Florent Perronnin, Jorge S ?anchez, and Thomas Mensink. Improving the fisher kernel for large-scale image classification. In Computer Vision–ECCV 2010, pages 143–156. Springer, 2010.
• [10] Josef Sivic and Andrew Zisserman. Video google: A text retrieval approach to object matching in videos. In Computer Vision, 2003. Proceedings. Ninth IEEE International Conference on, pages 1470–1477. IEEE, 2003.
• [11] Jan C van Gemert, Cor J Veenman, Arnold WM Smeulders, and J-M Geusebroek. Visual word ambiguity. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 32(7):1271–1283, 2010.
• [12] Simon Winder, Gang Hua, and Matthew Brown. Picking the best daisy. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on, pages 178–185. IEEE, 2009.
• [13] Simon AJ Winder and Matthew Brown. Learning local image descriptors. In Computer Vision and Pattern Recognition, 2007. CVPR’07. IEEE Conference on, pages 1–8. IEEE, 2007.

Aggregating local features for Image Retrieval

标签：

原文地址：http://www.cnblogs.com/jeromeblog/p/4181862.html