正则表达式引擎

时间：2014-12-27 17:31:34 阅读：248 评论：0 收藏：0 [点我收藏+]

标签：

一、前言

1.1 正则表达式

正则表达式的概念最开始是由 Unix 中的工具软件 (如 sed 和 grep) 普及开的。正则表达式是对字符串操作的一种逻辑公式,就是用事先定义好的一些特定字符、及这些特定字符的
组合,组成一个“规则字符串”,这个“规则字符串”用来表达对字符串的一种过滤逻辑。给定一个正则表达式和另一个字符串,我们可以达到如下的目的:

给定的字符串是否符合正则表达式的过滤逻辑(称作“匹配”);
可以通过正则表达式,从字符串中获取我们想要的特定部分。

正则表达式的特点是:

灵活性、逻辑性和功能性非常的强;
可以迅速地用极简单的方式达到字符串的复杂控制。

由于正则表达式主要应用对象是文本,因此它在各种文本编辑器场合都有应用,小到著名编辑器 EditPlus,大到 Microsoft Word、Visual Studio 等大型编辑器,都可以使用正则表达式
来处理文本内容。[1]

正则表达式是一种文本模式,包含普通字符和特殊字符,其中特殊字符又称为“元字符”,元字符完整列表参见正则表达式列表。可以将元字符分为三类:

普通字符集合:通过标记表示多种普通字符,例如‘.’代表除换行符以外的其他任意字符。
定界字符:表示位置的一类字符,用于边界检测,例如‘%blatex%b’是用来匹配单词latex 的,是一种全词匹配。
控制字符:控制重复、分支以及分组的一类字符,例如‘*’表示重复 0 至任意次。

　　文本模式就是通过这些元字符、普通字符的组合来表示,使用这些字符可以以很简洁的形式表示某种字符串结构。正则表达式的作用不仅仅局限在文本的搜索匹配上,在网络安全 [2]、数据库查询 [3]、协议识别 [4] 等领域都有应用。

1.2 贪婪匹配

贪婪算法又称为贪心法,是一种比较简单的算法。与动态规划法类似,贪心法常用于求解问题的最优解。贪心法在解决问题的策略上是根据当前的已知信息做出决策,并且决策之后就不再改变。可见,贪心法并非是从全局最优考虑,而是局部最优,这种局部最优不能保证所求出的解是全局最优解,但是一般情况下是近似最优解。能用贪心法求得最优解的问题通常具有以下两种性质:

最优子结构。当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构。
贪心选择性质。全局最优解可以通过一系列的局部最优解的选择来得到。

使用贪心法解决的典型问题有排课问题 [5]、背包问题 [6] 和多机调度问题 [7]。

1.3 说明

仅仅要求匹配 ASCII 中的可显示字符。
不需要处理表意冲突的情况。
存在多个输出结果时, 仅仅匹配第一个输出结果。
不要求能识别错误的正则表达式。

二、算法设计

设计要求实现元字符和反义字符的匹配、重复匹配、分支匹配、分组匹配这几项基本功能。其中分组匹配只要求实现后项引用,可以使用字符串替换进行处理,此外,分支匹配也可以转换成多个标准模式字符串,那么实现标准模式字符串的匹配过程,就实现了整个模式字符串的匹配。其中标准模式字符串的定义如下:

定义 2.1 (标准模式字符串) 模式字符串中,不存在分支及分组,并且不存在多余的括号,括号只能在跟有重复项的情况下出现,这样的字符串称为标准模式字符串。

在对原始模式字符串的处理过程中,首先进行文本的预处理过程,预处理是为了得到标准模式字符串,然后进行标准模式字符串的匹配过程,其中预处理过程主要是字符串的处理过程。整体流程如下图所示:

技术分享

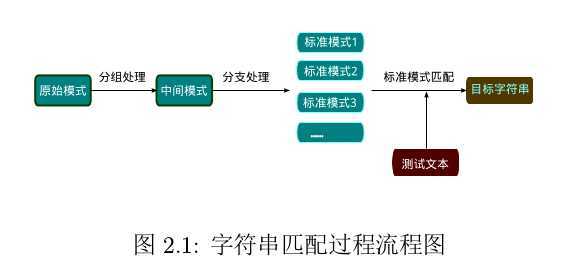
字符串匹配以标准模式字符串为界,前面一部分是字符串的转换过程,后一部分是匹配过程。下面将按照处理流程,分别阐述分组处理、分支处理、标准格式匹配三个步骤:

2.1 分组处理

正则表达式的分组使用一对括号‘(’、‘)’表示一个子表达式,这个子表达式为一个分组。每个分组都会分配一个组号,分配的规则为:从左向右, 以分组的左括号为标志, 第一个出现的分组的组号为 1, 第二个为 2, 以此类推。后向引用用于重复搜索前面某个分组匹配的文本。要得到无分组引用的模式字符串,需要将引用的子表达式替换掉引用记号。实现这一功能,需要分两步进行:

提取分组。从原始字符串中,提取出个子表达式,并且按照组号进行排列。
替换。用子表达式替换所有的引用记号。

提取文本中的分组是一种括号匹配问题,对于这类问题通常使用栈实现。实现算法如下:

struct Slice{
    int index;
    string value;
    int ter;
    int start;
};
typedef vector<Slice> VecSlice;

VecSlice getSliceOfPattern(string s, VecInt & vertex) {
    VecSlice vSlice;
    string value;
    value = "";
    Slice slice;
    stack<int> bra;
    int index = 0;
    vertex.push_back(-1);
    while (index < s.size()) {
        if (isSeparator(s[index])) {
            slice.value = value;
            value = "";
            slice.ter = index;
            slice.start = index - slice.value.size() - 1;
            vertex.push_back(index);
            switch (s[index]) {
            case ‘(‘:
                vSlice.push_back(slice);
                slice.index = index;
                bra.push(index);
                break;
            case ‘)‘:
                vSlice.push_back(slice);
                slice.index = index;
                bra.pop();
                break;
            case ‘|‘:
                vSlice.push_back(slice);
                if (bra.size() == 0)
                    slice.index = -1;
                else
                    slice.index = bra.top();
                break;
            }

        } else
            value = value + s[index];
        index++;
    }
    slice.value = value;
    slice.ter = index;
    slice.start = slice.ter - value.size() - 1;
    vSlice.push_back(slice);
    vertex.push_back(index);
    for (uint i = 0; i < vSlice.size(); ++i) {
        vSlice[i].index = findInVertex(vSlice[i].index, vertex);
        vSlice[i].start = findInVertex(vSlice[i].start, vertex);
        vSlice[i].ter = findInVertex(vSlice[i].ter, vertex);
    }

    return vSlice;
}

取得模式字符串中的分组后,下面就是引用的替换了,替换过程比较简单,首先查找引用标记,然后用相应的子表达式做替换,如此循环替换下去,直到模式字符串中不再有引用标记为止。

2.2 分支处理

前面一节已经完成了分组处理的过程,下面将需要进行分支处理。对于一个如下形式的模式字符串:

ab((c|d)e|f )g (2.1)

将其转换成状态图形式如下(此处不同考虑重复情况,括号后面跟有重复定义时,不会改变其重复意义):

技术分享

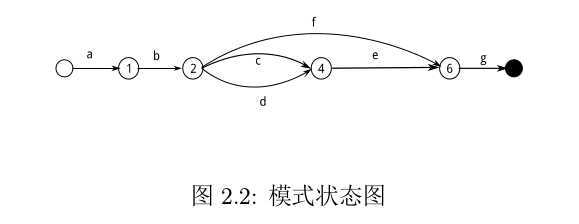
为了便于描述,定义位置的索引如下图所示:

技术分享

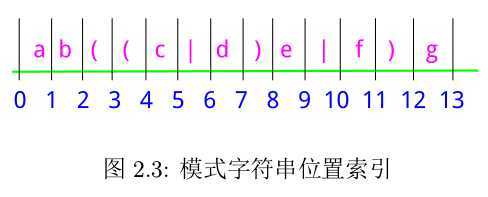
将模式字符串分成几段,其分段列表如下:

技术分享

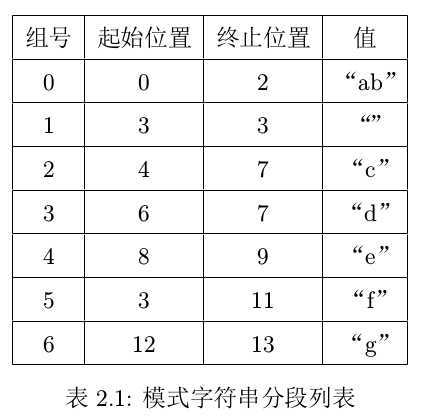
注意:分支中的各分支的起始位置与终止位置相同。

可以看到,将各段按起始位置有序连接,就是图 2.2 的简化版。以图论的观点看,这是有向图无环图(DAG,) 找路径的问题 [8]。但是相对于一般的有向无环图来说,它具有一些特性:

只有两个顶点没有出度或者入度,其他的顶点都有出度和入度,并且只有出度的顶点是起始点,只有入度的顶点是终点。
此图不可分割。图中各顶点都连接在一起,是一个连通图。
此图中的每一个顶点都可以通过特定的路径到达终点。

上面一个例子的 DAG 图如下:

技术分享

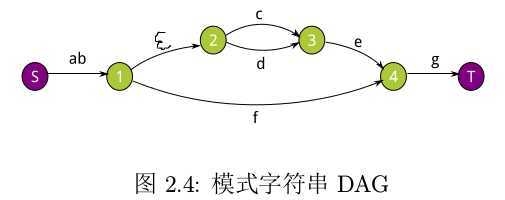
使用邻接表存储,则此 DAG 图的邻接表的结构如下图所示:

技术分享

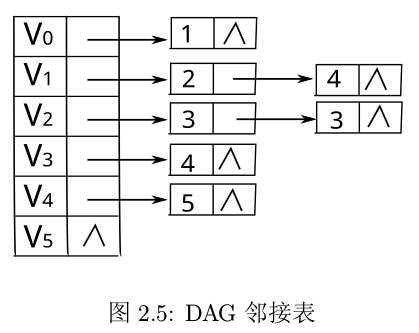
以这个图为例,算法处理过程如下表所示:

技术分享

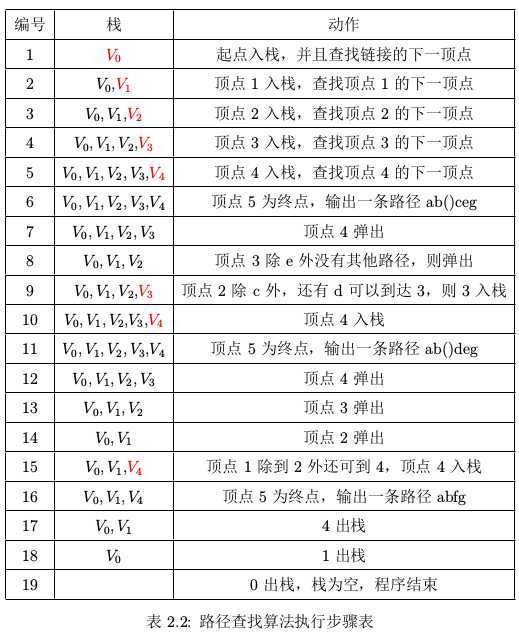
上述的处理过程,需要对访问的节点进行标记,对于已经回退的节点需要及时清除标记。

2.3 标准模式匹配

前面两节已经进行了预处理过程,已经得到了标准模式字符串的列表。这部分将对标准模式匹配过程进行阐述,标准模式匹配分模式字符串解析和字符串检测两部分,下面将分这两
部分描述。

2.3.1 模式字符串解析

在解析模式字符串之前先剔除不必要的括号,这个过程较为简单,在此略过。分析元字符,将其分成几大类,在头文件中定义其类型码:

1 //模式类型码
2 #define     PATTERN_NORMAL        11    //\w  \s  \d  [x]
3 #define    PATTERN_NOT        12    //\W \S \D [^x] ‘.‘
4 #define    PATTERN_REPEAT        13    //重复类型
5 #define     PATTERN_POS_WORD    14    //\b
6 #define     PATTERN_POS_ENDLINE    15    //$
7 #define     PATTERN_POS_BENGINLINE    16    //^
8 #define     PATTERN_POS_NOTWORD    17    //\B

对于普通字字符、普通类型、取反类型的字符,表示的是一类字符,将使用字符区间表示可取的字符,其形式如 [[a-z][A-Z]......]。定义字符区间如下:

1 //可行域,即字符区间 [c_s,c_e]
2 struct CharInterval {
3 public:
4     char c_s;//起始
5     char c_e;//终止
6 };
7 typedef list<CharInterval> CInterval;

对于重复类型,需要指定重复的起始位置、终止位置、最小重复次数、最大重复次数。其中重复类型 *、+ 的最大重复次数是任意次数,用 -1 指定。综合以上考虑,定义模式单元数
据结构如下:

 1 struct PNode {
 2 public:
 3     CInterval charInterval;//当type=PATTERN_POS/PATTERN_REPEAT时为空
 4     int type;//类型 PATTERN_NORMAL/PATTERN_NOT/PATTERN_POS/PATTERN_REPEAT
 5     int repeat_min;//最小次数
 6     int repeat_max;//最大次数
 7     int repeat_s;//重复起点
 8     int repeat_e;//重复终点
 9     int repeat_level;//记录重复次数，在匹配时使用
10     PNode() {
11         this->charInterval = CInterval();
12         this->type = PATTERN_NORMAL;
13         this->repeat_min = this->repeat_max = 0;
14         this->repeat_e=this->repeat_s=0;
15         this->repeat_level=-1;
16     }
17 };

定义好数据结构,接下来就需要进行模式字符串的解析。模式字符串的解析, 采用预测分析的方法进行解析:

  1 uint index = 0;
  2     stack<int> stBraket;
  3     int bra, ket;
  4     bra = -1;
  5     ket = -1;
  6     while (index < regtxt.size()) {
  7         PNode pNode;
  8         switch (regtxt[index]) {
  9         case ‘^‘:
 10                 .......
 11         case ‘$‘:
 12             .......
 13             //小括号
 14         case ‘(‘:
 15             .......
 16         case ‘)‘:
 17            .......
 18             //中括号
 19         case ‘[‘:
 20            .......
 21             //大括号
 22         case ‘{‘:
 23             pNode.type = PATTERN_REPEAT;
 24             if (regtxt[index - 1] == ‘)‘) {
 25                 pNode.repeat_s = bra;
 26                 pNode.repeat_e = ket;
 27             } else {
 28                 pNode.repeat_e = vPattern.size() - 1;
 29                 pNode.repeat_s = pNode.repeat_e;
 30             }
 31             bra = -1;
 32             ket = -1;
 33             index++;
 34             int num;
 35             num = 0;
 36             while (regtxt[index] <= ‘9‘ && regtxt[index] >= ‘0‘) {
 37                 num = num * 10 + (regtxt[index] - ‘0‘);
 38                 index++;
 39             }
 40             pNode.repeat_min = num;
 41             num = 0;
 42             switch (regtxt[index]) {
 43             case ‘,‘:
 44                 index++;
 45                 if (regtxt[index] == ‘}‘) {
 46                     pNode.repeat_max = -1;
 47                 } else {
 48                     while (regtxt[index] <= ‘9‘ && regtxt[index] >= ‘0‘) {
 49                         num = num * 10 + (regtxt[index] - ‘0‘);
 50                         index++;
 51                     }
 52                     pNode.repeat_max = num;
 53                 }
 54                 break;
 55             case ‘}‘:
 56                 pNode.repeat_max = pNode.repeat_min;
 57                 break;
 58             }
 59             vPattern.push_back(pNode);
 60             break;
 61         case ‘*‘:
 62             pNode.type = PATTERN_REPEAT;
 63             pNode.repeat_min = 0;
 64             pNode.repeat_max = -1;
 65  
 66             if (regtxt[index - 1] == ‘)‘) {
 67                 pNode.repeat_s = bra;
 68                 pNode.repeat_e = ket;
 69             } else {
 70                 pNode.repeat_e = vPattern.size() - 1;
 71                 pNode.repeat_s = pNode.repeat_e;
 72             }
 73             bra = -1;
 74             ket = -1;
 75             vPattern.push_back(pNode);
 76             break;
 77         case ‘?‘:
 78             pNode.type = PATTERN_REPEAT;
 79             pNode.repeat_min = 0;
 80             pNode.repeat_max = 1;
 81  
 82             if (regtxt[index - 1] == ‘)‘) {
 83                 pNode.repeat_s = bra;
 84                 pNode.repeat_e = ket;
 85             } else {
 86                 pNode.repeat_e = vPattern.size() - 1;
 87                 pNode.repeat_s = pNode.repeat_e;
 88             }
 89             bra = -1;
 90             ket = -1;
 91             vPattern.push_back(pNode);
 92             break;
 93         case ‘+‘:
 94             ......
 95         case ‘.‘:
 96             .......
 97         case ‘\\‘://元字符
 98             index++;
 99             switch (regtxt[index]) {
100             case ‘w‘:
101                 ........
102             case ‘W‘:
103                 ........
104             case ‘s‘:
105                .........
106             case ‘S‘:
107                 ........
108             case ‘d‘:
109                 .........
110             case ‘D‘:
111                 ........
112             case ‘b‘:
113                 .......
114             case ‘B‘:
115                .....
116             default:
117                 string s;
118                 s = "出现不能处理的元字符\\" + regtxt[index];
119                 throw SelfException(s);
120                 break;
121             }
122             break;
123         default://常规字符
124             pNode.type = PATTERN_NORMAL;
125             string s;
126             s = regtxt[index];
127             pNode.charInterval = getCharInterval(s);
128             vPattern.push_back(pNode);
129             break;
130         }
131         index++;
132     }
133     sort(this->vRepeat.begin(), this->vRepeat.end(), greaterRepeat);

2.3.2 字符串的检测

字符串的检测首先要解决的问题是重复项的匹配问题,要求使用贪婪匹配,则从最长重复次数到最短重复次数进行遍历检测。以最外层重复子表达式为界,将表达式分为前中后三部分。字符串的前部则不存重复项,只需依次检测即可。中间部分是重复单元,对其进行遍历检测,在每一次循环中,都是一个标准模式字符串,同样将其分为前中后三部分,如此进行下去,最后分块的结果是只有前部,中间部分、及后部都为空。后部的处理跟中间部分类似。容易知道解决这种问题的最简单的方法是使用递归。

定义一个函数处理模式序列的分块,其定义如下:

 1 void Scanner::splitPattern(VecPattern vSource, VecPattern& pre,
 2         VecPattern& mid, VecPattern& post) {
 3     int len;
 4     len = vSource.size();
 5     VecInt flag;
 6     for (int i = 0; i < len; ++i) {
 7         flag.push_back(0);
 8     }
 9     for (int i = 0; i < len; ++i) {
10         if (vSource[i].type == PATTERN_REPEAT) {
11             for (int j = vSource[i].repeat_s; j <= vSource[i].repeat_e; ++j) {
12                 flag[j] = flag[j] + 1;
13             }
14         }
15     }
16     //前部
17     int i;
18     int k;
19     i = 0;
20     while (i < len) {
21         if (flag[i] == 0)
22             pre.push_back(vSource[i]);
23         else
24             break;
25         i++;
26     }
27     k = i;
28     while (i < len) {
29         if (flag[i] == 0)
30             break;
31         else
32             mid.push_back(vSource[i]);
33         i++;
34     }
35     if(mid.size()>0){
36         mid.push_back(vSource[i]);
37         i++;
38     }
39     for (uint i = 0; i < mid.size(); ++i) {
40         if (mid[i].type == PATTERN_REPEAT) {
41             mid[i].repeat_e = mid[i].repeat_e - k;
42             mid[i].repeat_s = mid[i].repeat_s - k;
43         }
44     }
45     k = i;
46     while (i < len) {
47         post.push_back(vSource[i]);
48         i++;
49     }
50     for (uint j = 0; j < post.size(); ++j) {
51         if (post[j].type == PATTERN_REPEAT) {
52             post[j].repeat_e = post[j].repeat_e - k;
53             post[j].repeat_s = post[j].repeat_s - k;
54         }
55     }
56 }

前部字符串检测函数定义如下:

 1 bool Scanner::pvsMatch(int & beg, VecPattern vPat, string s) {
 2     if (vPat.size() == 0)
 3         return true;
 4     if (beg >= s.size())
 5         return false;
 6     uint cache;
 7     cache = beg;
 8     uint flag;
 9     flag = 0;
10     while ( flag < vPat.size()) {
11         bool bBreak;
12         bBreak = false;
13         switch (vPat[flag].type) {
14         case PATTERN_NORMAL:
15             if(cache >= s.size())
16                 return false;
17             if (isInRange(s[cache], vPat[flag].charInterval)) {
18                 cache++;
19                 flag++;
20             } else {
21                 return false;
22             }
23             break;
24         case PATTERN_NOT:
25             if(cache >= s.size())
26                     return false;
27             if (isInRange(s[cache], vPat[flag].charInterval)) {
28                 return false;
29             } else {
30                 cache++;
31                 flag++;
32             }
33             break;
34         case PATTERN_POS_BENGINLINE:
35             if (isBeginOfLine(cache, s)) {
36                 flag++;
37             } else
38                 return false;
39             break;
40         case PATTERN_POS_ENDLINE:
41             if (cache==s.size())
42                 flag++;
43             else if(s[cache]==‘\n‘) {
44                 flag++;
45             } else
46                 return false;
47             break;
48         case PATTERN_POS_NOTWORD:
49             if (isWordBoder(cache, s)) {
50                 return false;
51             } else
52                 flag++;
53             ;
54             break;
55         case PATTERN_POS_WORD:
56             if (isWordBoder(cache, s)) {
57                 flag++;
58             } else
59                 return false;
60             break;
61         case PATTERN_REPEAT:
62             throw SelfException("此处不能处理重复项");
63             break;
64         default:
65             throw SelfException("未知类型项，检查type赋值语句");
66             break;
67         }
68     }
69     if(flag==vPat.size())
70         beg = cache;
71     return true;
72 }

中部匹配函数定义如下:

 1 bool Scanner::midMatch(int & beg, int min,int max, VecPattern vP, string s) {
 2     if(vP.size()==0)
 3         return true;
 4     int l,i;
 5     int first;
 6     first=beg;
 7     if(max==-1)
 8         l=s.size()-beg;
 9     else
10         l=max;
11     while(l>=min){
12         for(i=0;i<l;++i)
13             if(!postMatch(first,vP,s))
14                 break;
15         if(i==l)
16         {
17             beg=first;
18             return true;
19         }
20         else
21             first=beg;
22         l--;
23     }
24     if(l<min)
25         return false;
26     return false;
27 }

后部匹配过程定义如下:

 1 bool Scanner::postMatch(int & beg, VecPattern vP, string s) {
 2     int first=beg;
 3     if(vP.size()==0)
 4         return true;
 5     VecPattern vPvs, vPost, vMid;
 6     //TODO 分块    vPvs,vPost,vMid
 7     splitPattern(vP,vPvs,vMid,vPost);
 8     if(vMid.size()==0){
 9         if(pvsMatch(first,vPvs,s)){
10             beg=first;
11             return true;
12         }
13     }
14     else
15     if(pvsMatch(first,vPvs,s)){
16         PNode p(vMid.back());
17         vMid.pop_back();
18         if(midMatch(first,p.repeat_min,p.repeat_max,vMid,s))
19         {
20             if(postMatch(first,vPost,s))
21             {
22                 beg=first;
23                 return true;
24             }
25             else
26                 return false;
27         }
28         else
29             return false;
30     }else
31         return false;;
32 }

上述三个程序段分别定义了三个部分的匹配过程,其中 postMatch 是函数调用的起点,然后进行递归调用。这样就实现了标准模式字符串的匹配过程。

正则表达式引擎

标签：

原文地址：http://www.cnblogs.com/bacazy/p/4188585.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行