标签：
目录
1.卡尔曼滤波简介
2.基本模型
2.1系统模型
2.2观测模型
3.预测与更新
3.1预测方程
3.2更新方程
4.matlab实现
卡尔曼滤波要做的是：
已知：
系统的初始状态 x0
每个时间的测量 Z
系统模型和测量模型
求解：
状态x随着时间变化而产生的值
卡尔曼滤波模型假设k时刻的真实状态是从(k − 1)时刻的状态演化而来，符合下式：
(1)
(2)
时刻k，对真实状态 xk的一个测量zk满足下式:
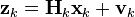(3)
其中Hk是观测模型,它把真实状态空间映射成观测空间，vk 是观测噪声，其均值为零，协方差矩阵为Rk,且服从正态分布。
(4)
初始状态以及每一时刻的噪声{x0, w1, ..., wk, v1 ... vk} 都认为是互相独立的.
预测是这样一个问题：
已知:
求解：
过程包括两个方面：
一、由上一个更新值 Xk-1|k-1 预测这一个预测值 Xk|k-1
二、由上一个更新值和真实值之间的误差 Pk-1|k-1 预测下一个预测值和真实值之间的误差 Pk|k-1
具体来说，就是以下两个方程。
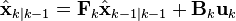(预测状态) (5)
(预测估计协方差矩阵) (6)
这里：
Xk-1|k-1 这种记法代表的是上一次的更新值，后面一个 k-1可以看做 Zk-1， 也就是上一次经过对比Zk-1(实际就是更新)之后所估计出的状态Xk-1。
Xk|k-1 这种记法代表这一次的预测值， 同理于刚才的介绍， 经过上一次Zk-1之后所估计出的状态Xk。
预测公式-预测状态
也就是公式(5)， 可以直接由系统模型导出。
预测公式-协方差矩阵：
P代表着估计误差的协方差，代表着一种 confidence ，比如先验估计误差(预测值与真实值之间误差)的协方差
更新过程实际上就是一下问题：
已知：
求解：
更新方程如下：
其中K称为kalman增益， 就像一个补偿，决定着预测值应该变化多少幅度，才能变成更新值。
1 %本例子从百度文库中得到， 稍加注释 2 clear 3 N=200;%取200个数 4 5 %% 生成噪声数据 计算噪声方差 6 w=randn(1,N); %产生一个1×N的行向量，第一个数为0，w为过程噪声（其和后边的v在卡尔曼理论里均为高斯白噪声） 7 w(1)=0; 8 Q=var(w); % R、Q分别为过程噪声和测量噪声的协方差(此方程的状态只有一维，方差与协方差相同) 9 10 v=randn(1,N);%测量噪声 11 R=var(v); 12 13 %% 计算真实状态 14 x_true(1)=0;%状态x_true初始值 15 A=1;%a为状态转移阵，此程序简单起见取1 16 for k=2:N 17 x_true(k)=A*x_true(k-1)+w(k-1); %系统状态方程，k时刻的状态等于k-1时刻状态乘以状态转移阵加噪声（此处忽略了系统的控制量） 18 end 19 20 21 %% 由真实状态得到测量数据， 测量数据才是能被用来计算的数据， 其他都是不可见的 22 H=0.2; 23 z=H*x_true+v;%量测方差，c为量测矩阵，同a简化取为一个数 24 25 26 %% 开始 预测-更新过程 27 28 % x_predict: 预测过程得到的x 29 % x_update:更新过程得到的x 30 % P_predict:预测过程得到的P 31 % P_update:更新过程得到的P 32 33 %初始化误差 和 初始位置 34 x_update(1)=x_true(1);%s(1)表示为初始最优化估计 35 P_update(1)=0;%初始最优化估计协方差 36 37 for t=2:N 38 %-----1. 预测----- 39 %-----1.1 预测状态----- 40 x_predict(t) = A*x_update(t-1); %没有控制变量 41 %-----1.2 预测误差协方差----- 42 P_predict(t)=A*P_update(t-1)*A‘+Q;%p1为一步估计的协方差，此式从t-1时刻最优化估计s的协方差得到t-1时刻到t时刻一步估计的协方差 43 44 %-----2. 更新----- 45 %-----2.1 计算卡尔曼增益----- 46 K(t)=H*P_predict(t) / (H*P_predict(t)*H‘+R);%b为卡尔曼增益，其意义表示为状态误差的协方差与量测误差的协方差之比(个人见解) 47 %-----2.2 更新状态----- 48 x_update(t)=x_predict(t) + K(t) * (z(t)-H*x_predict(t));%Y(t)-a*c*s(t-1)称之为新息，是观测值与一步估计得到的观测值之差，此式由上一时刻状态的最优化估计s(t-1)得到当前时刻的最优化估计s(t) 49 %-----2.3 更新误差协方差----- 50 P_update(t)=P_predict(t) - H*K(t)*P_predict(t);%此式由一步估计的协方差得到此时刻最优化估计的协方差 51 end 52 53 %% plot 54 %作图，红色为卡尔曼滤波，绿色为量测，蓝色为状态 55 %kalman滤波的作用就是 由绿色的波形得到红色的波形， 使之尽量接近蓝色的真实状态。 56 t=1:N; 57 plot(t,x_update,‘r‘,t,z,‘g‘,t,x_true,‘b‘);
标签：
原文地址：http://www.cnblogs.com/void0/p/4189821.html
