标签:
一直以为梯度下降很简单的,结果最近发现我写的一个梯度下降特别慢,后来终于找到原因:step size的选择很关键,有一种叫backtracking line search的梯度下降法就非常高效,该算法描述见下图:

下面用一个简单的例子来展示,给一个无约束优化问题:
minimize y = (x-3)*(x-3)
下面是python代码,比较两种方法
# -*- coding: cp936 -*- #optimization test, y = (x-3)^2 from matplotlib.pyplot import figure, hold, plot, show, xlabel, ylabel, legend def f(x): "The function we want to minimize" return (x-3)**2 def f_grad(x): "gradient of function f" return 2*(x-3) x = 0 y = f(x) err = 1.0 maxIter = 300 curve = [y] it = 0 step = 0.1 #下面展示的是我之前用的方法,看上去貌似还挺合理的,但是很慢 while err > 1e-4 and it < maxIter: it += 1 gradient = f_grad(x) new_x = x - gradient * step new_y = f(new_x) new_err = abs(new_y - y) if new_y > y: #如果出现divergence的迹象,就减小step size step *= 0.8 err, x, y = new_err, new_x, new_y print ‘err:‘, err, ‘, y:‘, y curve.append(y) print ‘iterations: ‘, it figure(); hold(True); plot(curve, ‘r*-‘) xlabel(‘iterations‘); ylabel(‘objective function value‘) #下面展示的是backtracking line search,速度很快 x = 0 y = f(x) err = 1.0 alpha = 0.25 beta = 0.8 curve2 = [y] it = 0 while err > 1e-4 and it < maxIter: it += 1 gradient = f_grad(x) step = 1.0 while f(x - step * gradient) > y - alpha * step * gradient**2: step *= beta x = x - step * gradient new_y = f(x) err = y - new_y y = new_y print ‘err:‘, err, ‘, y:‘, y curve2.append(y) print ‘iterations: ‘, it plot(curve2, ‘bo-‘) legend([‘gradient descent I used‘, ‘backtracking line search‘]) show()
运行结果如下图:
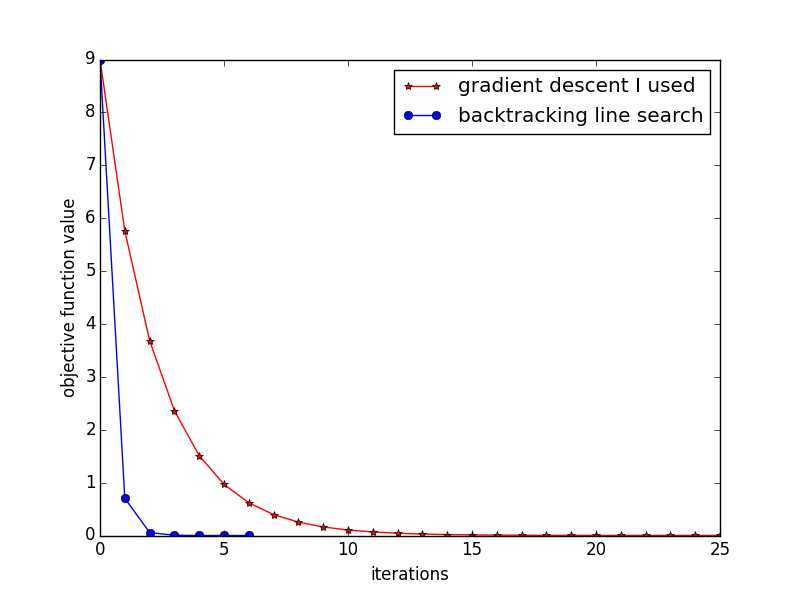
孰优孰劣,一目了然
我的方法用了25次迭代,而backtracking line search只用了6次。(而且之前我用的方法不一定会收敛的,比如你把第一种方法的stepsize改成1,就会发现,没有收敛到最优解就停止了,这是一个bug,要注意)
这只是个toy example,在我真实使用的优化问题上,两者的效率差别更加显著,估计有10倍的样子
--
文章中截图来自:https://www.youtube.com/watch?v=nvZF-t2ltSM
(是cmu的优化课程)
重新发现梯度下降法--backtracking line search
标签:
原文地址:http://www.cnblogs.com/fstang/p/4192735.html