标签:
一直拖、放了放久、受不了
Description
Input
Output
Sample Input
2 1 #. .# 4 4 ...# ..#. .#.. #... -1 -1
Sample Output
2 1
思路:DFS
#include <iostream> #include <cstdio> #include <cstring> using namespace std; #define ll long long #define N 10 int n,k; int ans; int col[N]; char mpt[N][N]; void dfs(int row,int num) { if(num==k) { ans++; return; } if(row>n) return; dfs(row+1,num); for(int j=1;j<=n;j++) { if(mpt[row][j]==‘#‘ && !col[j]) { col[j]=1; dfs(row+1,num+1); col[j]=0; } } } int main() { while(scanf("%d%d",&n,&k)!=EOF) { if(n==-1 && k==-1) break; ans=0; memset(col,0,sizeof(col)); for(int i=1;i<=n;i++) { scanf("%s",mpt[i]+1); } dfs(1,0); cout<<ans<<endl; } return 0; }
Description
Input
Output
Escaped in x minute(s).
Trapped!
Sample Input
3 4 5 S.... .###. .##.. ###.# ##### ##### ##.## ##... ##### ##### #.### ####E 1 3 3 S## #E# ### 0 0 0
Sample Output
Escaped in 11 minute(s). Trapped!
思路:三维BFS
#include <iostream> #include <cstdio> #include <queue> #include <cstring> using namespace std; #define mod 1000000007 #define ll long long #define N 50 struct node { int x,y,z,t; }; int n,m,k; int x,y,z; int vis[N][N][N]; char mpt[N][N][N]; int dir[6][3]={1,0,0,-1,0,0,0,1,0,0,-1,0,0,0,1,0,0,-1}; bool judge(int x,int y,int z) { if(x<1 || x>n || y<1 || y>m || z<1 || z>k) return 0; if(mpt[x][y][z]==‘#‘) return 0; if(vis[x][y][z]) return 0; return 1; } void bfs() { queue<node> q; memset(vis,0,sizeof(vis)); node now,next; now.x=x; now.y=y; now.z=z; now.t=0; vis[x][y][z]=1; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(mpt[now.x][now.y][now.z]==‘E‘) { printf("Escaped in %d minute(s).\n",now.t); return; } for(int i=0;i<6;i++) { next=now; next.x+=dir[i][0]; next.y+=dir[i][1]; next.z+=dir[i][2]; if(judge(next.x,next.y,next.z)) { next.t++; vis[next.x][next.y][next.z]=1; q.push(next); } } } cout<<"Trapped!\n"; } int main() { while(scanf("%d%d%d",&n,&m,&k),n+m+k) { for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { for(int l=1;l<=k;l++) { scanf(" %c",&mpt[i][j][l]); if(mpt[i][j][l]==‘S‘) { x=i; y=j; z=l; } } } } bfs(); } return 0; }
Description
Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.
* Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
* Teleporting: FJ can move from any point X to the point 2 × X in a single minute.
If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?
Input
Output
Sample Input
5 17
Sample Output
4
Hint
#include <iostream> #include <cstdio> #include <queue> #include <cstring> using namespace std; #define mod 1000000007 #define ll long long #define N 100000 int n,m; int vis[N+10]; void bfs(int s) { memset(vis,0,sizeof(vis)); queue<pair<int,int>> q; pair<int,int> now,next; now.first=s; now.second=0; vis[s]=1; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(now.first==m) { cout<<now.second<<endl; return; } for(int i=1;i<=3;i++) { next=now; next.second++; if(i==1) next.first-=1; else if(i==2) next.first+=1; else if(i==3) next.first*=2; if(next.first>=0 && next.first<=N && !vis[next.first]) { vis[next.first]=1; q.push(next); } } } } int main() { while(scanf("%d%d",&n,&m)!=EOF) { if(n==m) { cout<<0<<endl; continue; } bfs(n); } return 0; }
Description
Farmer John knows that an intellectually satisfied cow is a happy cow who will give more milk. He has arranged a brainy activity for cows in which they manipulate an M × N grid (1 ≤ M ≤ 15; 1 ≤ N ≤ 15) of square tiles, each of which is colored black on one side and white on the other side.
As one would guess, when a single white tile is flipped, it changes to black; when a single black tile is flipped, it changes to white. The cows are rewarded when they flip the tiles so that each tile has the white side face up. However, the cows have rather large hooves and when they try to flip a certain tile, they also flip all the adjacent tiles (tiles that share a full edge with the flipped tile). Since the flips are tiring, the cows want to minimize the number of flips they have to make.
Help the cows determine the minimum number of flips required, and the locations to flip to achieve that minimum. If there are multiple ways to achieve the task with the minimum amount of flips, return the one with the least lexicographical ordering in the output when considered as a string. If the task is impossible, print one line with the word "IMPOSSIBLE".
Input
Output
Sample Input
4 4 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
Sample Output
0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0
思路:枚举第一行状态+模拟
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> #include <string> #include <map> using namespace std; #define INF 0xfffffff #define ll long long #define N 20 int n,m; int res; int mpt[N][N]; //原始状态 int ans[N][N]; //保存答案 int tmp[N][N]; //翻转模拟数组 int vis[N][N]; //记录是否翻转 void flip(int i,int j) { tmp[i][j]^=1; if(i-1>=0) tmp[i-1][j]^=1; if(i+1<n) tmp[i+1][j]^=1; if(j-1>=0) tmp[i][j-1]^=1; if(j+1<m) tmp[i][j+1]^=1; } int solve() { for(int i=1;i<n;i++) { for(int j=0;j<m;j++) { if(tmp[i-1][j]) flip(i,j),vis[i][j]=1; } } int time=0; for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { time+=vis[i][j]; if(tmp[i][j]) return INF; } } return time; } int main() { int i,j,k; while(scanf("%d%d",&n,&m)!=EOF) { res=INF; for(i=0;i<n;i++) { for(j=0;j<m;j++) { scanf("%d",&mpt[i][j]); } } int MAX=1<<m; for(k=0;k<MAX;k++) //枚举第一行的状态 { memset(vis,0,sizeof(vis)); memcpy(tmp,mpt,sizeof(mpt)); for(j=0;j<m;j++) { if(k&(1<<j)) flip(0,j),vis[0][j]=1; } int time=solve(); if(time<res) { res=time; memcpy(ans,vis,sizeof(vis)); } } if(res==INF) cout<<"IMPOSSIBLE\n"; else { for(i=0;i<n;i++) { for(j=0;j<m;j++) { if(j) cout<<‘ ‘; cout<<ans[i][j]; } cout<<endl; } } } return 0; }
Description
Input
Output
Sample Input
2 6 19 0
Sample Output
10 100100100100100100 111111111111111111
思路:BFS
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> #include <string> using namespace std; #define ll long long int n; void bfs() { queue<ll> q; q.push(1); while(1) { ll sum=q.front(); if(sum%n==0) { cout<<sum<<endl; return; } q.pop(); q.push(10*sum); q.push(10*sum+1); } } int main() { while(cin>>n,n) { bfs(); } return 1; }
Description
 The ministers of the cabinet were quite upset by the message from the Chief of Security stating that they would all have to change the four-digit room numbers on their offices.
The ministers of the cabinet were quite upset by the message from the Chief of Security stating that they would all have to change the four-digit room numbers on their offices. 1033The cost of this solution is 6 pounds. Note that the digit 1 which got pasted over in step 2 can not be reused in the last step – a new 1 must be purchased.
1733
3733
3739
3779
8779
8179
Input
Output
Sample Input
3 1033 8179 1373 8017 1033 1033
Sample Output
6 7 0
思路:BFS
#include <iostream> #include <cstdio> #include <queue> #include <cstring> using namespace std; #define mod 1000000007 #define ll long long #define N 110 struct node { int x,t; }; int n,m; int vis[10005]; bool judge(int n) { if(vis[n]) return 0; if(n==1) return 0; for(int i=2;i*i<=n;i++) { if(n%i==0) return 0; } return 1; } void bfs() { int i,j,tmp[5]; queue<node> q; memset(vis,0,sizeof(vis)); node now,next; now.x=n; now.t=0; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(now.x==m) { cout<<now.t<<endl; return; } int tp=now.x,k=4; while(tp) { tmp[k--]=tp%10; tp/=10; } for(i=0;i<4;i++) { next=now; next.t++; if(i==0) { for(j=1;j<10;j++) { next.x=j*1000+tmp[2]*100+tmp[3]*10+tmp[4]; if(judge(next.x)) { vis[next.x]=1; q.push(next); } } } else if(i==1) { for(j=0;j<10;j++) { next.x=tmp[1]*1000+j*100+tmp[3]*10+tmp[4]; if(judge(next.x)) { vis[next.x]=1; q.push(next); } } } else if(i==2) { for(j=0;j<10;j++) { next.x=tmp[1]*1000+tmp[2]*100+j*10+tmp[4]; if(judge(next.x)) { vis[next.x]=1; q.push(next); } } } else { for(j=1;j<10;j++) { next.x=tmp[1]*1000+tmp[2]*100+tmp[3]*10+j; if(judge(next.x)) { vis[next.x]=1; q.push(next); } } } } } } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); bfs(); } return 0; }
Description
A common pastime for poker players at a poker table is to shuffle stacks of chips. Shuffling chips is performed by starting with two stacks of poker chips,S1 and S2, each stack containing C chips. Each stack may contain chips of several different colors.
The actual shuffle operation is performed by interleaving a chip from S1 with a chip from S2 as shown below for C = 5:
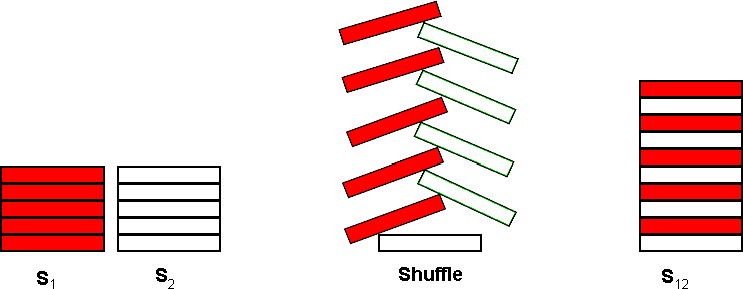
The single resultant stack, S12, contains 2 * C chips. The bottommost chip of S12 is the bottommost chip from S2. On top of that chip, is the bottommost chip from S1. The interleaving process continues taking the 2nd chip from the bottom of S2 and placing that on S12, followed by the 2nd chip from the bottom of S1 and so on until the topmost chip from S1 is placed on top of S12.
After the shuffle operation, S12 is split into 2 new stacks by taking the bottommost C chips from S12 to form a new S1 and the topmost C chips from S12to form a new S2. The shuffle operation may then be repeated to form a new S12.
For this problem, you will write a program to determine if a particular resultant stack S12 can be formed by shuffling two stacks some number of times.
Input
The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset consists of four lines of input. The first line of a dataset specifies an integer C, (1 ≤ C ≤ 100) which is the number of chips in each initial stack (S1 and S2). The second line of each dataset specifies the colors of each of the C chips in stack S1, starting with the bottommost chip. The third line of each dataset specifies the colors of each of the C chips in stack S2 starting with the bottommost chip. Colors are expressed as a single uppercase letter (Athrough H). There are no blanks or separators between the chip colors. The fourth line of each dataset contains 2 * C uppercase letters (A through H), representing the colors of the desired result of the shuffling of S1 and S2 zero or more times. The bottommost chip’s color is specified first.
Output
Output for each dataset consists of a single line that displays the dataset number (1 though N), a space, and an integer value which is the minimum number of shuffle operations required to get the desired resultant stack. If the desired result can not be reached using the input for the dataset, display the value negative 1 (−1) for the number of shuffle operations.
Sample Input
2 4 AHAH HAHA HHAAAAHH 3 CDE CDE EEDDCC
Sample Output
1 2 2 -1
思路:模拟+map标记
include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> #include <string> #include <map> using namespace std; #define ll long long int len; int ans; string s,e; string s1,s2; void shuffle() { s.clear(); for(int i=0;i<len;i++) { s+=s2[i]; s+=s1[i]; } } int solve() { int res=2; map<string,bool> m; while(m.find(s)==m.end()) //满足条件就表示出现过了 { m[s]=true; s1=s.substr(0,len); s2=s.substr(len,len); shuffle(); if(s==e) return res; res++; } return -1; } int main ( ) { int T,iCase=1; scanf("%d",&T); while(T--) { cin>>len; cin>>s1>>s2>>e; shuffle(); if(s==e) ans=1; else ans=solve(); cout<<iCase++<<" "<<ans<<endl; } return 0; }
Description
You are given two pots, having the volume of A and B liters respectively. The following operations can be performed:
Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots.
Input
On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B).
Output
The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’.
Sample Input
3 5 4
Sample Output
6 FILL(2) POUR(2,1) DROP(1) POUR(2,1) FILL(2) POUR(2,1)
思路:BFS+路径输出
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> #include <string> using namespace std; #define ll long long #define INF 0x7fffffff #define MOD 1000007 #define N 110 struct node { int a,b,t; string s; }; int A,B,C; int vis[N][N]; void pour(node &t,int k) { if(k==1) { if(B-t.b>=t.a) t.b+=t.a,t.a=0; else t.a-=(B-t.b),t.b=B; } else { if(A-t.a>=t.b) t.a+=t.b,t.b=0; else t.b-=(A-t.a),t.a=A; } } void show(string s) { int len=s.size(); for(int i=0;i<len;i++) { if(s[i]==‘1‘) printf("FILL(1)\n"); else if(s[i]==‘2‘) printf("FILL(2)\n"); else if(s[i]==‘3‘) printf("DROP(1)\n"); else if(s[i]==‘4‘) printf("DROP(2)\n"); else if(s[i]==‘5‘) printf("POUR(1,2)\n"); else if(s[i]==‘6‘) printf("POUR(2,1)\n"); } } void bfs() { node now,next; queue<node> q; memset(vis,0,sizeof(vis)); now.a=0; now.b=0; now.t=0; now.s=""; vis[0][0]=1; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(now.a==C || now.b==C) { printf("%d\n",now.t); show(now.s); return; } for(int i=1;i<=6;i++) { next=now; next.t++; if(i==1) next.a=A,next.s+=‘1‘; else if(i==2) next.b=B,next.s+=‘2‘; else if(i==3) next.a=0,next.s+=‘3‘; else if(i==4) next.b=0,next.s+=‘4‘; else if(i==5) pour(next,1),next.s+=‘5‘; else if(i==6) pour(next,2),next.s+=‘6‘; if(!vis[next.a][next.b]) { q.push(next); vis[next.a][next.b]=1; } } } printf("impossible\n"); } int main() { while(scanf("%d%d%d",&A,&B,&C)!=EOF) { bfs(); } return 0; }
Description
Fat brother and Maze are playing a kind of special (hentai) game on an N*M board (N rows, M columns). At the beginning, each grid of this board is consisting of grass or just empty and then they start to fire all the grass. Firstly they choose two grids which are consisting of grass and set fire. As we all know, the fire can spread among the grass. If the grid (x, y) is firing at time t, the grid which is adjacent to this grid will fire at time t+1 which refers to the grid (x+1, y), (x-1, y), (x, y+1), (x, y-1). This process ends when no new grid get fire. If then all the grid which are consisting of grass is get fired, Fat brother and Maze will stand in the middle of the grid and playing a MORE special (hentai) game. (Maybe it’s the OOXX game which decrypted in the last problem, who knows.)
You can assume that the grass in the board would never burn out and the empty grid would never get fire.
Note that the two grids they choose can be the same.
Input
The first line of the date is an integer T, which is the number of the text cases.
Then T cases follow, each case contains two integers N and M indicate the size of the board. Then goes N line, each line with M character shows the board. “#” Indicates the grass. You can assume that there is at least one grid which is consisting of grass in the board.
1 <= T <=100, 1 <= n <=10, 1 <= m <=10
Output
For each case, output the case number first, if they can play the MORE special (hentai) game (fire all the grass), output the minimal time they need to wait after they set fire, otherwise just output -1. See the sample input and output for more details.
Sample Input
Sample Output
Case 1:1
思路:枚举两起点BFS
#include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <queue> using namespace std; #define ll long long #define INF 0x7fffffff #define MOD 1000007 #define N 12 struct node { int x,y,t; }; int tot; int n,m; int vis[N][N]; char mpt[N][N]; node start[N*N]; queue<node> q; int dir[4][2]={1,0,-1,0,0,1,0,-1}; int bfs() { node now,next; while(!q.empty()) { now=q.front(); q.pop(); for(int i=0;i<4;i++) { next=now; next.t++; next.x+=dir[i][0]; next.y+=dir[i][1]; if(next.x>=1 && next.x<=n && next.y>=1 && next.y<=m && !vis[next.x][next.y] && mpt[next.x][next.y]==‘#‘) { q.push(next); vis[next.x][next.y]=1; } } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(mpt[i][j]==‘#‘ && !vis[i][j]) { return INF; } } } return now.t; } int main() { int T,iCase=1; scanf("%d",&T); while(T--) { tot=0; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%s",mpt[i]+1); } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(mpt[i][j]==‘#‘) { start[++tot].x=i; start[tot].y=j; start[tot].t=0; } } } int ans=INF; for(int i=1;i<=tot;i++) { for(int j=i;j<=tot;j++) { while(!q.empty()) q.pop(); memset(vis,0,sizeof(vis)); q.push(start[i]); vis[start[i].x][start[i].y]=1; q.push(start[j]); vis[start[j].x][start[j].y]=1; ans=min(ans,bfs()); } } if(ans==INF) ans=-1; printf("Case %d: %d\n",iCase++,ans); } return 0; }
Description
 Joe works in a maze. Unfortunately, portions of the maze have caught on fire, and the owner of the maze neglected to create a fire escape plan. Help Joe escape the maze.
Joe works in a maze. Unfortunately, portions of the maze have caught on fire, and the owner of the maze neglected to create a fire escape plan. Help Joe escape the maze.
Given Joe‘s location in the maze and which squares of the maze are on fire, you must determine whether Joe can exit the maze before the fire reaches him, and how fast he can do it.
Joe and the fire each move one square per minute, vertically or horizontally (not diagonally). The fire spreads all four directions from each square that is on fire. Joe may exit the maze from any square that borders the edge of the maze. Neither Joe nor the fire may enter a square that is occupied by a wall.
2 4 4 #### #JF# #..# #..# 3 3 ### #J. #.F
3 IMPOSSIBLE
思路:额有点坑、可能有多处火、加到队列BFS
#include <iostream> #include <cstdio> #include <cstring> #include <queue> using namespace std; #define INF 1<<30 #define N 1010 struct JF { int x,y,t; JF(){} JF(int x,int y,int t):x(x),y(y),t(t){} }; int n,m; int jx,jy; queue<JF> q; int vis[N][N]; int fire[N][N]; //fire[i][j]表示火到i,j位置的最短时间 char mpt[N][N]; int dir[4][2]={1,0,-1,0,0,1,0,-1}; bool judge(int x,int y) { if(x<1 || x>n || y<1 || y>m) return 0; if(mpt[x][y]==‘#‘) return 0; return 1; } void bfs1() { JF now,next; while(!q.empty()) { now=q.front(); q.pop(); for(int i=0;i<4;i++) { next=now; next.t++; next.x+=dir[i][0]; next.y+=dir[i][1]; if(judge(next.x,next.y)) { if(next.t<fire[next.x][next.y]) { fire[next.x][next.y]=next.t; q.push(next); } } } } } void bfs2() { queue<JF> q; memset(vis,0,sizeof(vis)); JF now,next; now.x=jx; now.y=jy; now.t=0; vis[jx][jy]=1; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(now.x==1 || now.x==n || now.y==1 || now.y==m) { cout<<now.t+1<<endl; return; } for(int i=0;i<4;i++) { next=now; next.t++; next.x+=dir[i][0]; next.y+=dir[i][1]; if(judge(next.x,next.y) && !vis[next.x][next.y] && fire[next.x][next.y]-next.t>=1) { vis[next.x][next.y]=1; q.push(next); } } } cout<<"IMPOSSIBLE\n"; } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%s",mpt[i]+1); } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { fire[i][j]=INF; if(mpt[i][j]==‘F‘) { fire[i][j]=0; q.push(JF(i,j,0)); } else if(mpt[i][j]==‘J‘) { jx=i; jy=j; } } } bfs1(); bfs2(); } return 0; }
Description
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
Input
Output
Sample Input
0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0
Sample Output
(0, 0) (1, 0) (2, 0) (2, 1) (2, 2) (2, 3) (2, 4) (3, 4) (4, 4)
思路:BFS+路径输出
#include <iostream> #include <cstdio> #include <queue> #include <cstring> using namespace std; #define mod 1000000007 #define ll long long #define N 10 struct node { int x,y,t,pre; }; struct queue { node q[1010]; int front,rear; }q; int n=5; int vis[N][N]; int mpt[N][N]; int dir[4][2]={1,0,-1,0,0,1,0,-1}; void show(int now) { int path[1010],len=0; path[++len]=now; while(q.q[now].pre!=-1) { path[++len]=q.q[now].pre; now=q.q[now].pre; } for(int i=len;i>=1;i--) { cout<<‘(‘<<q.q[path[i]].x-1<<", "<<q.q[path[i]].y-1<<‘)‘<<endl; } } void bfs() { q.front=q.rear=0; memset(vis,0,sizeof(vis)); node now,next; now.x=1; now.y=1; now.t=0; now.pre=-1; vis[1][1]=1; q.q[++q.rear]=now; while(q.front!=q.rear) { now=q.q[++q.front]; if(now.x==n && now.y==n) { show(q.front); return; } for(int i=0;i<4;i++) { next=now; next.x+=dir[i][0]; next.y+=dir[i][1]; if(next.x>=1 && next.x<=n && next.y>=1 && next.y<=n && !vis[next.x][next.y] && !mpt[next.x][next.y]) { next.t++; next.pre=q.front; vis[next.x][next.y]=1; q.q[++q.rear]=next; } } } } int main() { while(scanf("%d",&mpt[1][1])!=EOF) { for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==1 && j==1) continue; scanf("%d",&mpt[i][j]); } } bfs(); } return 0; }
Description
Input
Output
Sample Input
Sample Output
#include <iostream> #include <cstdio> #include <queue> #include <cstring> using namespace std; #define mod 1000000007 #define ll long long #define N 110 int n,m; char mpt[N][N]; int dir[8][2]={1,1,-1,-1,1,-1,-1,1,1,0,-1,0,0,1,0,-1}; void DFS(int x,int y) { for(int i=0;i<8;i++) { int tx=x+dir[i][0]; int ty=y+dir[i][1]; if(tx>=1 && ty>=1 && tx<=n && ty<=m && mpt[tx][ty]==‘@‘) { mpt[tx][ty]=‘*‘; DFS(tx,ty); } } } int main() { int i,j; while(scanf("%d%d",&n,&m)!=EOF) { if(n==0 && m==0) break; for(i=1;i<=n;i++) { scanf("%s",mpt[i]+1); } int ans=0; for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { if(mpt[i][j]==‘@‘) { ans++; mpt[i][j]=‘*‘; DFS(i,j); } } } cout<<ans<<endl; } return 0; }
Description
Input
Output
Sample Input
Sample Output
#include <iostream> #include <cstring> #include <queue> #include <cstdio> #include <algorithm> using namespace std; #define N 110 struct node { int w[3],t; }; int v[3]; int vis[N][N][N]; void pour(node &t,int i,int j) { if(v[j]-t.w[j]>=t.w[i]) { t.w[j]+=t.w[i]; t.w[i]=0; } else { t.w[i]-=(v[j]-t.w[j]); t.w[j]=v[j]; } } bool judge(int a,int b,int c) { if(a==0 && b==c) return 1; if(b==0 && a==c) return 1; if(c==0 && b==a) return 1; return 0; } void bfs() { node now,next; queue<node> q; memset(vis,0,sizeof(vis)); now.w[0]=v[0]; now.w[1]=0; now.w[2]=0; now.t=0; vis[v[0]][v[1]][v[2]]=1; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); if(judge(now.w[0],now.w[1],now.w[2])) { cout<<now.t<<endl; return; } for(int i=0;i<3;i++) { for(int j=0;j<3;j++) { if(i==j) continue; next=now; pour(next,i,j); if(!vis[next.w[0]][next.w[1]][next.w[2]]) { next.t++; vis[next.w[0]][next.w[1]][next.w[2]]=1; q.push(next); } } } } cout<<"NO\n"; } int main() { while(scanf("%d%d%d",&v[0],&v[1],&v[2]),v[0]+v[1]+v[2]) { bfs(); } return 0; }
Description
Input
Output
Sample Input
Sample Output
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <queue> using namespace std; #define INF 0x7ffffff #define N 220 struct node { int x,y,t; }; int n,m; int x[3],y[3]; char mpt[N][N]; int tmp[N][N][2]; int vis[N][N]; int dir[4][2]={1,0,-1,0,0,1,0,-1}; void bfs(int index) { queue<node> q; memset(vis,0,sizeof(vis)); node now,next; now.x=x[index]; now.y=y[index]; now.t=0; vis[x[index]][y[index]]=1; tmp[x[index]][y[index]][index]=0; q.push(now); while(!q.empty()) { now=q.front(); q.pop(); for(int i=0;i<4;i++) { next=now; next.x+=dir[i][0]; next.y+=dir[i][1]; if(next.x>=1 && next.x<=n && next.y>=1 && next.y<=m && !vis[next.x][next.y] && mpt[next.x][next.y]!=‘#‘) { next.t++; if(mpt[next.x][next.y]==‘@‘) tmp[next.x][next.y][index]=next.t; vis[next.x][next.y]=1; q.push(next); } } } } int main() { int i,j; while(scanf("%d%d",&n,&m)!=EOF) { for(i=1;i<=n;i++) scanf("%s",mpt[i]+1); for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { tmp[i][j][1]=tmp[i][j][2]=INF; if(mpt[i][j]==‘M‘) x[1]=i,y[1]=j; else if(mpt[i][j]==‘Y‘) x[2]=i,y[2]=j; } } bfs(1); bfs(2); int ans=INF; for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { if(mpt[i][j]==‘@‘) { ans=min(ans,tmp[i][j][1]+tmp[i][j][2]); } } } cout<<ans*11<<endl; } return 0; }
标签:
原文地址:http://www.cnblogs.com/hate13/p/4194730.html