标签:
题意:房间是一个凸多边形,要在里面铺设两条半径为r的圆形地毯,可以重叠,现在要求分别铺设到哪,使地毯所占的地面面积最大。
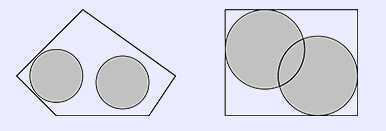
解法:要使圆形地毯所占面积最大,圆形地毯一定是与边相切的,这样才能使尽量不重叠。 那么我们把所有边都向内推进r,那么形成的多边形,可知两个圆形地毯的中心就一定在这个多边形边界上,最优的情况下是在此新凸包的最远点对上。
初始多边形为(-1000,-1000)到(1000,1000)的矩形,那么我们可以模拟把每条边都推进,每次切出新的凸多边形,然后得出最后的凸多边形,然后n^2枚举求最远点对即可。这里用到直线切割一个凸多边形的算法。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> #include <cmath> #include <algorithm> #define Mod 1000000007 #define pi acos(-1.0) #define eps 1e-8 using namespace std; struct Point{ double x,y; Point(double x=0, double y=0):x(x),y(y) {} void input() { scanf("%lf%lf",&x,&y); } }; typedef Point Vector; struct Line{ Point p; Vector v; double ang; Line(){} Line(Point p, Vector v):p(p),v(v) { ang = atan2(v.y,v.x); } Point point(double t) { return Point(p.x + t*v.x, p.y + t*v.y); } bool operator < (const Line &L)const { return ang < L.ang; } }; int dcmp(double x) { if(x < -eps) return -1; if(x > eps) return 1; return 0; } template <class T> T sqr(T x) { return x * x;} Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); } bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); } bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; } bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; } bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; } double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } double Length(Vector A) { return sqrt(Dot(A, A)); } double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); } double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; } Vector VectorUnit(Vector x){ return x / Length(x);} Vector Normal(Vector x) { return Point(-x.y, x.x) / Length(x);} double angle(Vector v) { return atan2(v.y, v.x); } Point GetLineIntersection(Line A, Line B) { Vector u = A.p - B.p; double t = Cross(B.v, u) / Cross(A.v, B.v); return A.p + A.v*t; } double DisP(Point A,Point B) { return Length(B-A); } int LineCrossPolygon(Point& L1,Point& L2,Point* p,int n,Point* poly) { int m = 0; for(int i=0,j;i<n;i++) { if(dcmp(Cross(L1-p[i],L2-p[i])) >= 0) { poly[m++] = p[i]; continue; } j = (i-1+n)%n; if(dcmp(Cross(L1-p[j],L2-p[j])) > 0) poly[m++] = GetLineIntersection(Line(L1,L2-L1),Line(p[j],p[i]-p[j])); j = (i+1+n)%n; if(dcmp(Cross(L1-p[j],L2-p[j])) > 0) poly[m++] = GetLineIntersection(Line(L1,L2-L1),Line(p[j],p[i]-p[j])); } return m; } Line L[122]; Point poly[3][124],p[140],q1,q2; int len[3]; int main() { int i,j,pre,now,n; double r; while(scanf("%d%lf",&n,&r)!=EOF) { poly[0][0] = Point(-1000,-1000); poly[0][1] = Point(1000,-1000); poly[0][2] = Point(1000,1000); poly[0][3] = Point(-1000,1000); len[pre = 0] = 4; for(i=0;i<n;i++) p[i].input(); for(i=0;i<n;i++) { now = pre^1; Vector nv = Normal(p[i]-p[(i+1)%n]); q1 = p[i] + nv*r; q2 = q1+p[(i+1)%n]-p[i]; len[now] = LineCrossPolygon(q2,q1,poly[pre],len[pre],poly[now]); pre = now; } double Maxi = -Mod; for(i=0;i<len[now];i++) for(j=i;j<len[now];j++) { if(dcmp(DisP(poly[now][i],poly[now][j])-Maxi) > 0) { Maxi = DisP(poly[now][i],poly[now][j]); q1 = poly[now][i], q2 = poly[now][j]; } } printf("%.6f %.6f %.6f %.6f\n",q1.x,q1.y,q2.x,q2.y); } return 0; }
标签:
原文地址:http://www.cnblogs.com/whatbeg/p/4198431.html