标签:
可持久化线段树是一种神奇的数据结构,它跟我们原来常用的线段树不同,它每次更新是不更改原来数据的,而是新开节点,维护它的历史版本,实现“可持久化”。(当然视情况也会有需要修改的时候)
可持久化线段树的应用有很多,仅以区间第K大这种简单的问题来介绍这种数据结构。
我们原本建立的线段树是表示区间的,或者说,维护的是【位置】,存的是每个位置上的各种信息。它的优点是满足区间加法,但不满足区间减法,所以我们这里要换一种建树方式:对于每个区间[1,i]建立一棵权值线段树。这个线段树的作用其实就跟前缀和差不多,且像前缀和一样满足区间减法!只不过我们在求前缀和的时候保留的是sum,而权值线段树把所有的值都存下来了。
这里说一下它的保存方式:对[1,x]这个节点,它需要维护一个cnt值,表示在[1,x]这个值域,有cnt个数。
举个栗子,我们现在有一个序列{1,2,3,4,5,2,3,3,3,3}
然后对于表示区间[1,10]的线段树,它的节点是这样建的
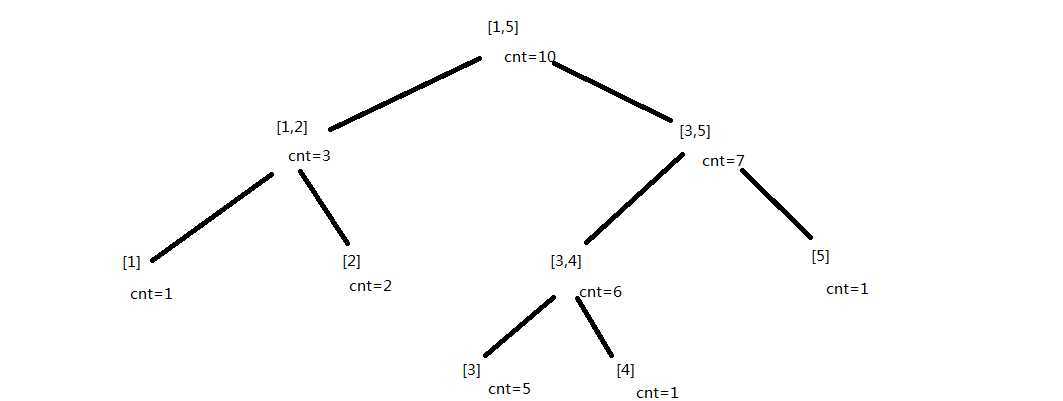
可以看出,值在[1,5]的有10个数,在[1,2]的有3个数……以此类推
那么我们在查询第K大的时候,就可以像平衡树那样!如果左儿子的cnt>=k则在左边找,否则在右边找,那么我们就可以顺利地查询到第K大了~
那么问题来了:如果我想查询[3,7]这个区间上第3大的数应该怎么办呢?(这个地方容易晕,一定要分清原序列的区间和值域,虽然都是用方括号的区间表示的……如果看了这句话更晕了,那就忘了它吧)
那么就要回到我们之前说的【前缀和】上来了,我们以前快速求[l,r]的区间和,是利用前缀和[1,l-1]和[1,r]区间相减快速计算的,同理,我们也可以利用[1,l-1]和[1,r]两棵线段树来进行区间第K大的查询。即在两棵树上同时往下走!详见代码。

1 //POJ 2104 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<iostream> 6 #include<algorithm> 7 #define rep(i,n) for(int i=0;i<n;++i) 8 #define F(i,j,n) for(int i=j;i<=n;++i) 9 #define D(i,j,n) for(int i=j;i>=n;--i) 10 using namespace std; 11 const int N=100086; 12 //#define debug 13 14 struct node{ 15 int x,num,rank; 16 }a[N]; 17 bool cmpx(node a,node b){ 18 return a.x<b.x; 19 } 20 bool cmpn(node a,node b){ 21 return a.num<b.num; 22 } 23 24 struct Tree{ 25 int cnt,l,r; 26 }t[N*30]; 27 int root[N],cnt=0,n,m; 28 29 #define mid (l+r>>1) 30 void updata(int &o,int l,int r,int pos){ 31 t[++cnt]=t[o], o=cnt, ++t[o].cnt; 32 if (l==r) return; 33 if (pos<=mid) updata(t[o].l,l,mid,pos); 34 else updata(t[o].r,mid+1,r,pos); 35 #ifdef debug 36 printf("%d %d %d %d\n",o,l,r,pos); 37 #endif 38 } 39 40 int query(int i,int j,int rank){ 41 i=root[i],j=root[j]; 42 int l=1,r=n; 43 while(l!=r){ 44 if (t[t[j].l].cnt-t[t[i].l].cnt>=rank)//在两棵树上一起往下走 45 r=mid,i=t[i].l,j=t[j].l; 46 else{ 47 rank-=t[t[j].l].cnt-t[t[i].l].cnt; 48 l=mid+1,i=t[i].r,j=t[j].r; 49 } 50 } 51 return l; 52 } 53 #undef mid 54 55 int main(){ 56 freopen("file.in","r",stdin); 57 scanf("%d%d",&n,&m); 58 int x=0; 59 F(i,1,n) {scanf("%d",&a[i].x); a[i].num=i;} 60 sort(a+1,a+n+1,cmpx); 61 F(i,1,n) a[i].rank=i; 62 sort(a+1,a+n+1,cmpn); 63 F(i,1,n) { 64 root[i]=root[i-1]; 65 updata(root[i],1,n,a[i].rank);//此处可以先不理解…… 66 //简单来说就是:为了节约空间,我们并不需要真的给每个区间建一棵完整的线段树 67 //而是可以在原来的基础上进行新的维护(即原来的为历史版本) 68 } 69 sort(a+1,a+n+1,cmpx); 70 F(i,1,m){ 71 int l,r,k; 72 scanf("%d%d%d",&l,&r,&k); 73 printf("%d\n",a[query(l-1,r,k)].x); 74 } 75 return 0; 76 }
标签:
原文地址:http://www.cnblogs.com/Tunix/p/4197815.html