标签:
题意:
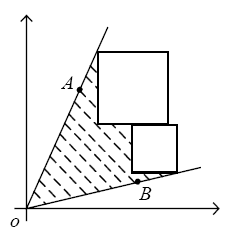
如图,有n个正方形和一个角(均在第一象限中),使这些正方形与这个角构成封闭的阴影区域,求阴影区域面积的最大值。
分析:
直观上来看,当这n个正方形的对角线在一条直线上时,封闭区域的面积最大。(虽然我不太会证明,=_=||)
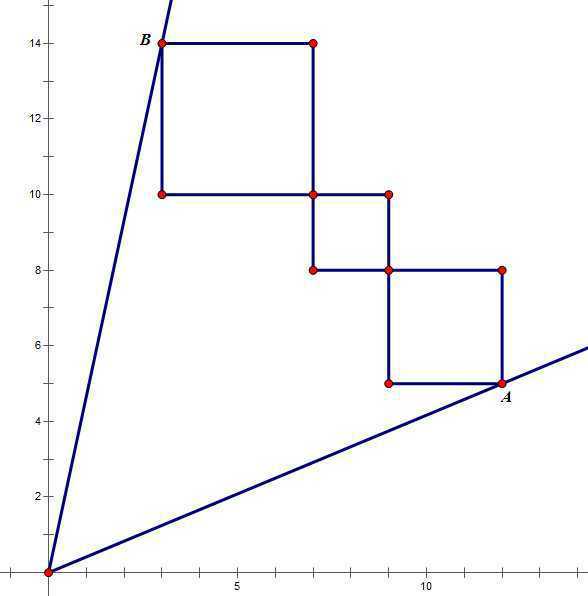
设所有正方形边长之和为L,OA、OB两直线方程分别为:y = k1x y = k2x,设A(x1, k1x1), B(x2, k2x2),可列出方程:
,解得
,相应的就得到AB两点坐标,用叉积算出△OAB的面积再减去这些正方形面积的一半就是答案。

1 #include <cstdio> 2 #include <algorithm> 3 4 struct Point 5 { 6 double x, y; 7 Point(double x=0, double y=0):x(x), y(y) {} 8 }; 9 10 double Cross(const Point& A, const Point& B) 11 { return A.x*B.y - A.y*B.x; } 12 13 int main() 14 { 15 //freopen("in.txt", "r", stdin); 16 int n; 17 while(scanf("%d", &n) == 1 && n) 18 { 19 Point A, B; 20 double L = 0, subArea = 0, l; 21 scanf("%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y); 22 for(int i = 0; i < n; ++i) 23 { 24 scanf("%lf", &l); 25 L += l; 26 subArea += l * l / 2; 27 } 28 double k1 = A.y / A.x, k2 = B.y / B.x; 29 if(k1 > k2) std::swap(k1, k2); 30 double x1 = (k1+1)*L/(k2-k1), y1 = k1 * x1; 31 double x2 = (k2+1)*L/(k2-k1), y2 = k2 * x2; 32 A = Point(x1, y1), B = Point(x2, y2); 33 double ans = Cross(A, B) / 2 - subArea; 34 35 printf("%.3f\n", ans); 36 } 37 38 return 0; 39 }
标签:
原文地址:http://www.cnblogs.com/AOQNRMGYXLMV/p/4205743.html