标签：
中国大陆数学界某些机构关于函数凹凸性定义和另一些机构不同。
那么我们来讲凸函数（convex function）为什么叫做是凸（convex）的：这是因为凸函数与凸集（convex set）有联系，而凸集的定义没有争议。
1. 凸函数与凸集通过 sublevel sets 这个概念联系起来。
首先来看一个函数的 sublevel sets。对于函数来说，它的
-sublevel set
是这样定义的:
也就是在函数定义域内，对应函数值小于的自变量的取值构成的集合。
联系1：对于任意来说，一个凸函数的
-sublevel set 是一个凸集。
注意该命题的逆命题不成立。为了更好的理解这个概念，以及逆命题为什么不成立，我们来看一个例子（图来自参考资料）：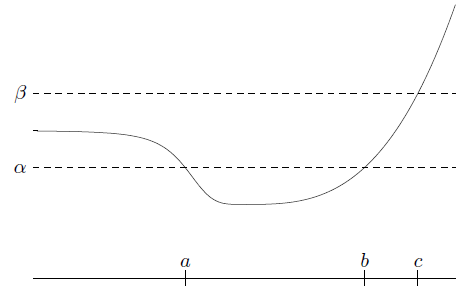
这是一个定义域和值域都在里面的函数，它是非凸的。它的
-sublevel set 就是
，显然是一个凸集。我们甚至可以看到对于这个函数，给定任意
它的
-sublevel set 都是凸集，但这个函数不是凸函数。这样的函数有一个名字叫做 quasiconvex.
2. 凸函数与凸集通过 epigraph 这个概念联系起来。
接着看一个函数的 epigraph。它是这样定义的：
这个前缀 epi 好像是 above 的意思，那么epigraph的意思大概是「上方的图」。对于的函数，它的 epigraph 就应该是
的子集。
接着看刚才的栗子，这个函数的epigraph就是函数上方的灰色部分（原谅我）：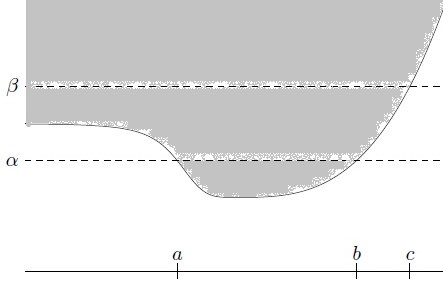
看到了吗，这不是一个凸集。
联系2：凸函数的 epigraph 是一个凸集，反之也成立。也就是说，一个函数是凸函数，当且仅当它的 epigraph 是凸集。
参考资料：
Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004.
-----------
突
然发现 sublevel sets 和 epigraph 这两个概念也是相对的，把 sublevel sets
定义的小于等于号换成大于等于号说不定就有了 "superlevel sets", 同样的还可以定义 "hypograph",
所以可能凹凸的分别还是 by convention吧？
from:http://www.zhihu.com/question/20014186
标签：
原文地址：http://www.cnblogs.com/lovepipi/p/4211805.html
