标签:
线性回归方法是机器学习里面最基础的一种方法,相关的理论方面的知识有很多,这里就不介绍了,博客主要从scikit-learn库的使用方面来探讨算法。
首先,我们使用随机生成一组数据,然后加入一些随机噪声。

1 import numpy as np 2 from sklearn.cross_validation import train_test_split 3 4 def f(x): 5 return np.sin(2 * np.pi * x) 6 7 x_plot = np.linspace(0, 1, 100) 8 9 n_samples = 100 10 X = np.random.uniform(0, 1, size=n_samples)[:, np.newaxis] 11 y = f(X) + np.random.normal(scale=0.3, size=n_samples)[:, np.newaxis] ##add random noise to the dataset 12 13 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.8)
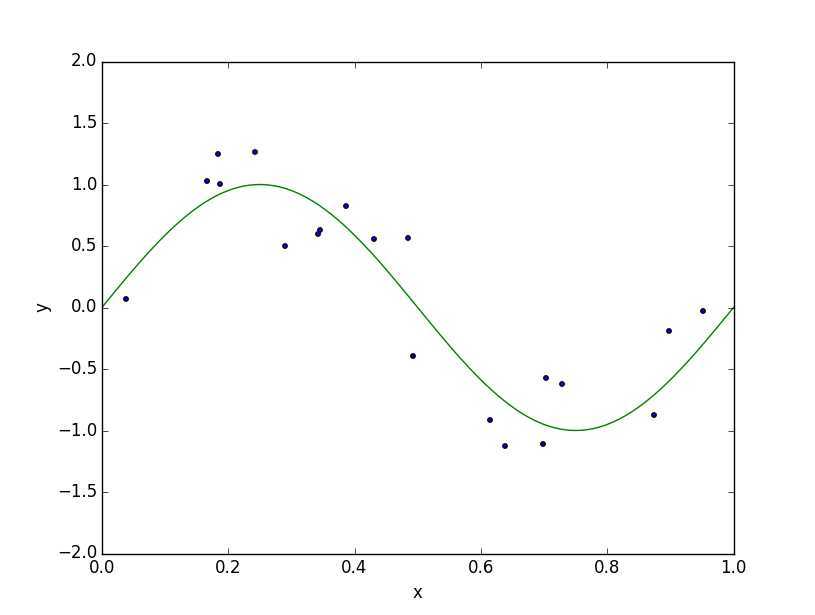
首先,不添加正则项

1 fig, axes = plt.subplots(5, 2, figsize=(8, 5)) 2 train_error = np.empty(10) 3 test_error = np.empty(10) 4 # 5 for ax, degree in zip(axes.ravel(), range(10)): 6 est = make_pipeline(PolynomialFeatures(degree), LinearRegression()) 7 est.fit(X_train, y_train) 8 train_error[degree] = mean_squared_error(y_train, est.predict(X_train)) 9 test_error[degree] = mean_squared_error(y_test, est.predict(X_test)) 10 plot_approximation(est, ax, label=‘degree=%d‘ %degree) 11 plt.show(fig) 12 13 plt.plot(np.arange(10), train_error, color=‘green‘, label=‘train‘) 14 plt.plot(np.arange(10), test_error, color=‘red‘, label=‘test‘) 15 plt.ylim(0.0, 1e0) 16 plt.ylabel(‘log(mean squared error)‘) 17 plt.xlabel(‘degree‘) 18 plt.legend(loc="upper left") 19 plt.show()
误差为:
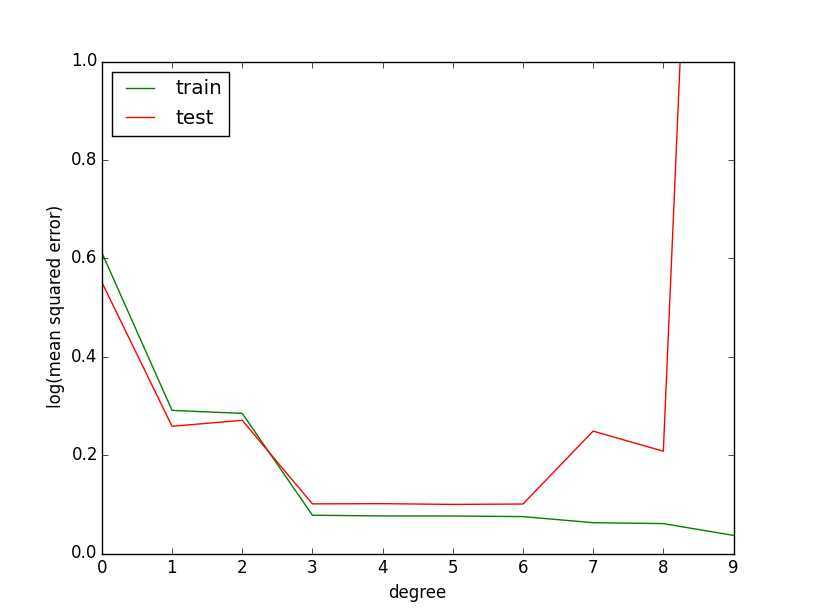
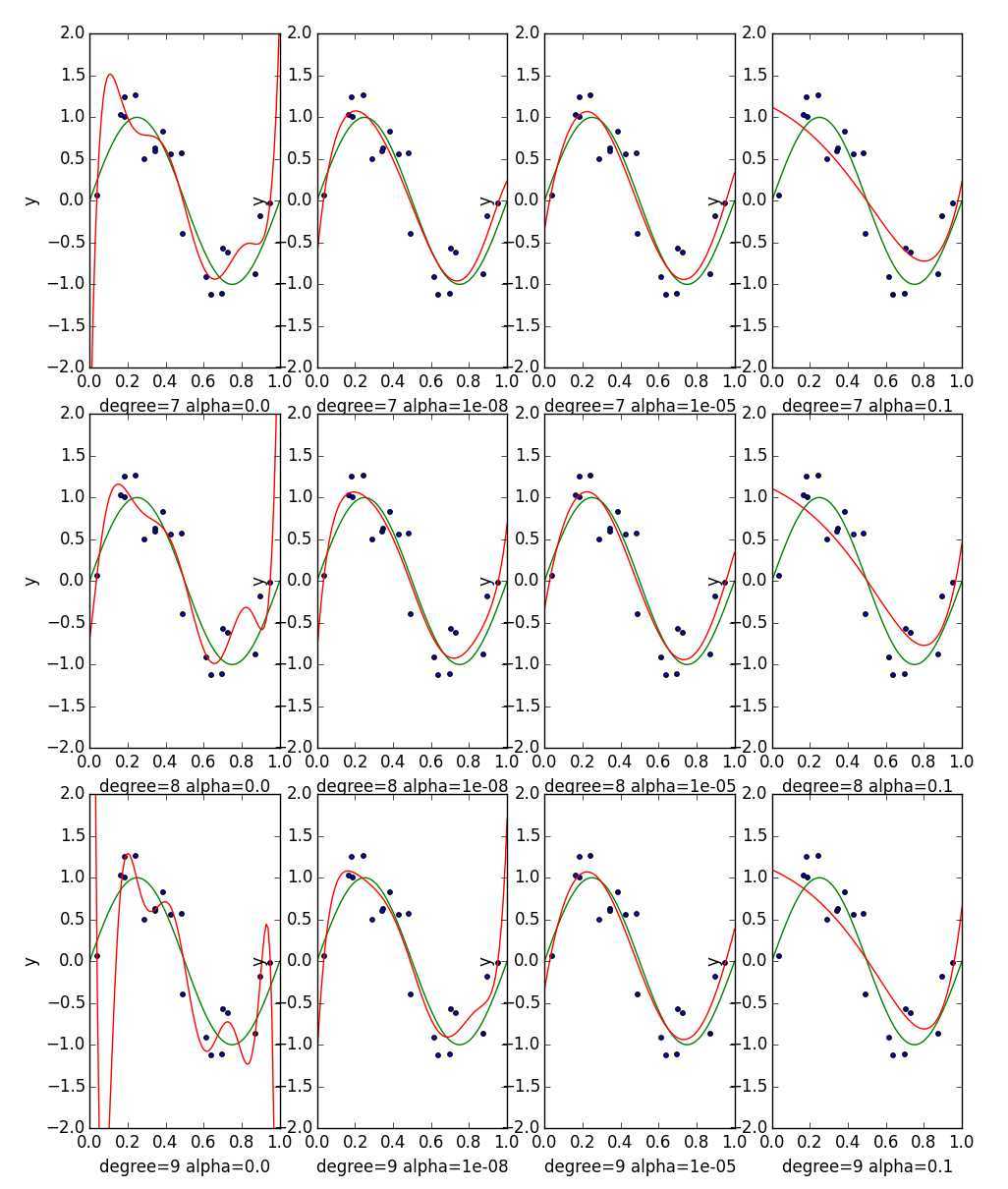
当多项式的最高次幂超过6之后,训练样本的误差小,测试样本的误差过大,出现了过拟合,下面加入L2正则项:

1 alphas = [0.0, 1e-8, 1e-5, 1e-1] 2 degree = 9 3 fig, ax_rows = plt.subplots(3, 4, figsize=(8, 5)) 4 for degree, ax_row in zip(range(7, 10), ax_rows): 5 for alpha, ax in zip(alphas, ax_row): 6 est = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=alpha)) 7 est.fit(X_train, y_train) 8 plot_approximation(est, ax, xlabel="degree=%d alpha=%r" %(degree, alpha)) 9 #plt.tight_layout() 10 plt.show(fig)
具体看看不同的alpha大小对多项式系数的影响:

1 def plot_coefficients(est, ax, label=None, yscale=‘log‘): 2 coef = est.steps[-1][1].coef_.ravel() 3 if yscale == ‘log‘: 4 ax.semilogy(np.abs(coef), marker=‘o‘, label=label) 5 ax.set_ylim((1e-1, 1e8)) 6 else: 7 ax.plot(np.abs(coef), marker=‘o‘, label=label) 8 ax.set_ylabel(‘abs(coefficient)‘) 9 ax.set_xlabel(‘coefficients‘) 10 ax.set_xlim((1, 9)) 11 12 fig, ax_rows = plt.subplots(4, 2, figsize=(8, 5)) 13 alphas = [0.0, 1e-8, 1e-5, 1e-1] 14 for alpha, ax_row in zip(alphas, ax_rows): 15 ax_left, ax_right = ax_row 16 est = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=alpha)) 17 est.fit(X_train, y_train) 18 plot_approximation(est, ax_left, label=‘alpha=%r‘%alpha) 19 plot_coefficients(est, ax_right, label=‘Ridge(alpha=%r) coefficients‘ % alpha ) 20 21 plt.show(fig)
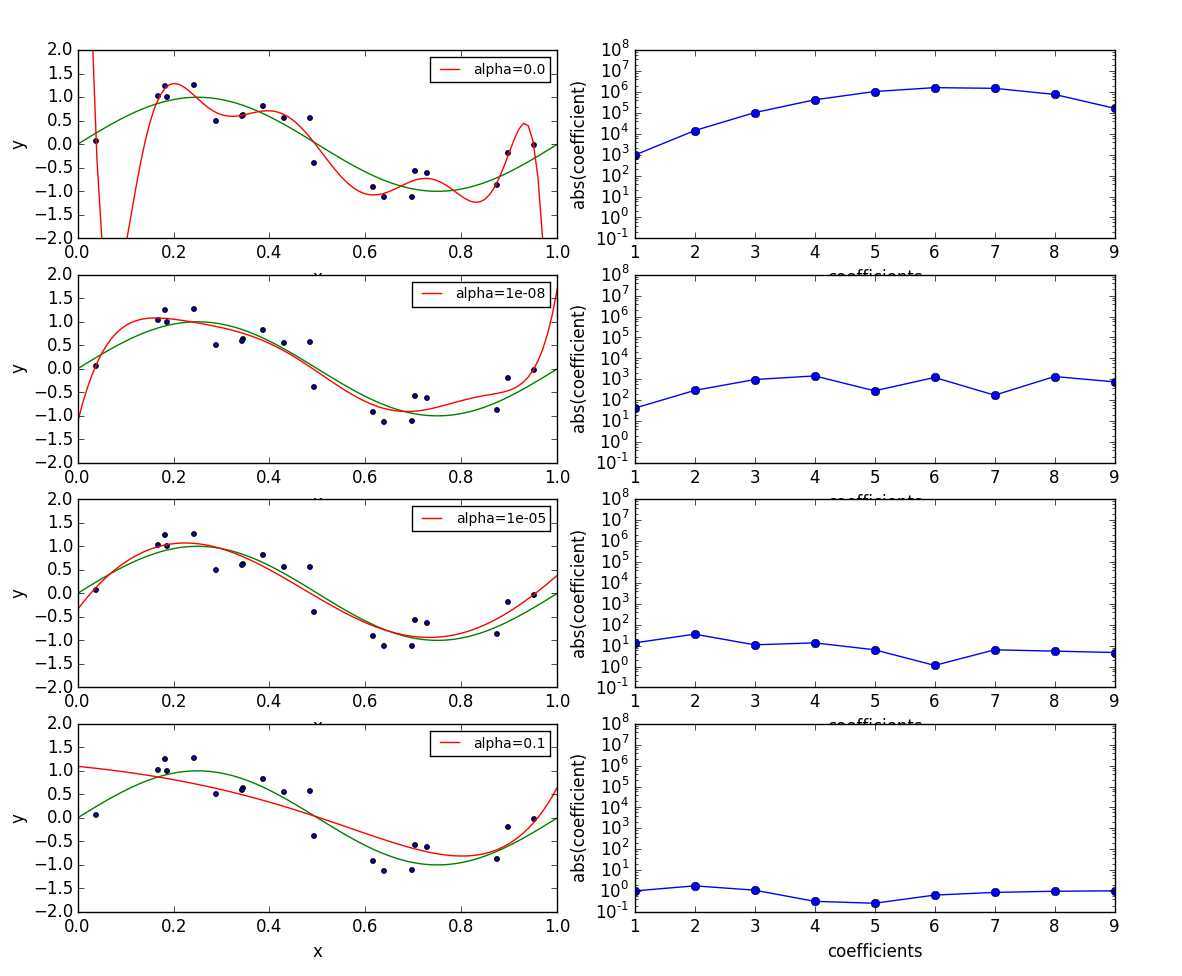
alpha越大,因子越小,而曲线也越来越平滑。使用Ridge,可以加入L2正则项,还可以通过使用Lasso,加入L1正则项

1 fig, ax_rows = plt.subplots(2, 2, figsize=(8, 5)) 2 3 degree = 9 4 alphas = [1e-3, 1e-2] 5 6 for alpha, ax_row in zip(alphas, ax_rows): 7 ax_left, ax_right = ax_row 8 est = make_pipeline(PolynomialFeatures(degree), Lasso(alpha=alpha)) 9 est.fit(X_train, y_train) 10 plot_approximation(est, ax_left, label=‘alpha=%r‘ % alpha) 11 plot_coefficients(est, ax_right, label=‘Lasso(alpha=%r) coefficients‘ % alpha, yscale=None) 12 13 plt.tight_layout() 14 plt.show(fig)
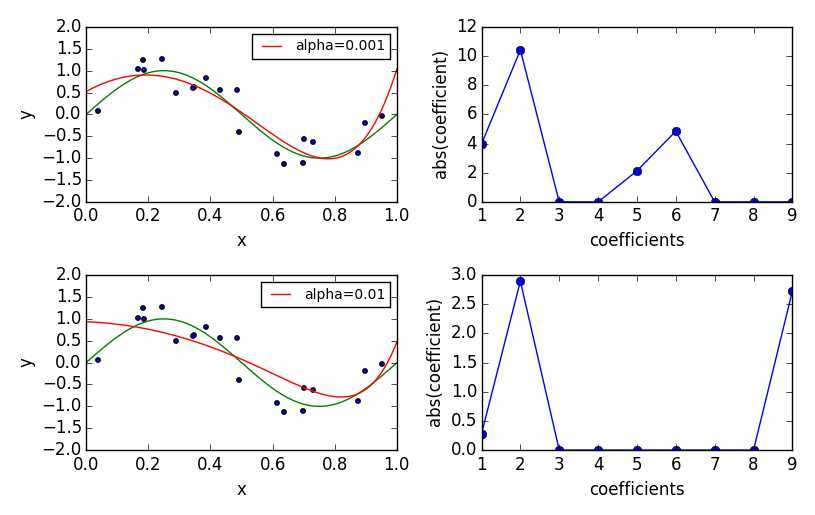
除了上述两种方式外,scikit-learn还支持同时加入L1和L2正则,需要使用ElasticNet进行训练

1 fig, ax_rows = plt.subplots(8, 2, figsize=(8, 5)) 2 alphas = [1e-2, 1e-2, 1e-2, 1e-3, 1e-3, 1e-3, 1e-4, 1e-4] 3 ratios = [0.05, 0.85, 0.50, 0.05, 0.85, 0.50, 0.03, 0.95] 4 for alpha, ratio, ax_row in zip(alphas, ratios, ax_rows): 5 ax_left, ax_right = ax_row 6 est = make_pipeline(PolynomialFeatures(degree), ElasticNet(alpha=alpha, l1_ratio=ratio)) 7 est.fit(X_train, y_train) 8 plot_approximation(est, ax_left, label=‘alpha=%r ratio=%r‘ % (alpha, ratio)) 9 plot_coefficients(est, ax_right, label="Lasso(alpah=%r ratio=%r) coefficients" % (alpha, ratio), yscale=None) 10 11 plt.show()
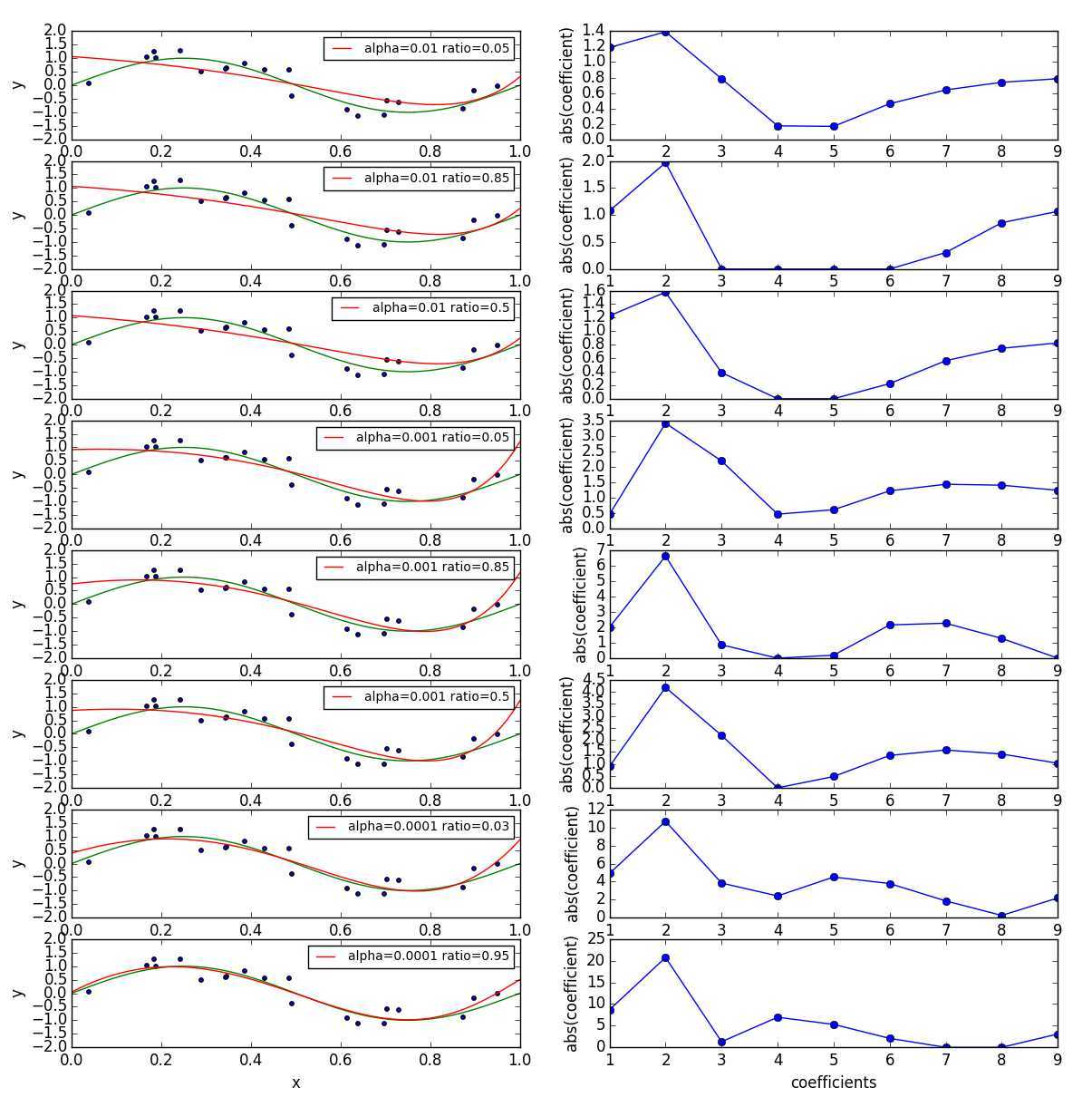
当alpha一定时,曲线形状并未发生明显变化,alpha限定了参数范围,alpha越小,参数取值范围越大,这与只使用L2、L1正则时相似。ratio决定了参数的取值情况,当ratio比较大时,则参数相对稀疏(只有少数几个参数的值比较大,而其余的值比较小者趋近于0),
而ratio比较小时,参数之间差异相对较小,分布较为均匀。
未完待续。。。
标签:
原文地址:http://www.cnblogs.com/bootstar/p/4212902.html