标签:
题目链接:http://www.lydsy.com:808/JudgeOnline/problem.php?id=2627
题意:计算下面式子
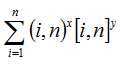
思路:

A先不管。我们来搞B部分。下面说如何计算B这个最后那部分
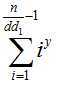
伯努利函数:
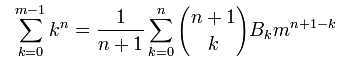
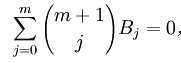
所以
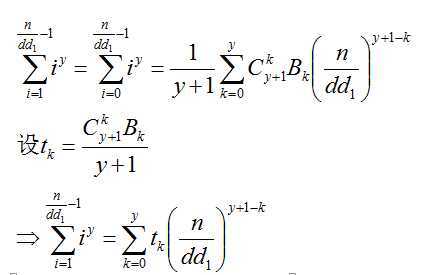
带入到B中
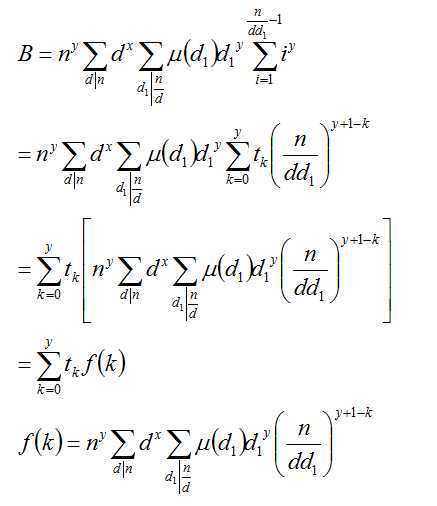
那个f(k)中k一旦确定x,y,k就是常数,所以就是关于n的函数。
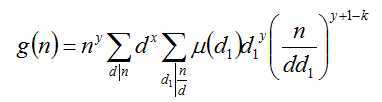
然后这个据说说积性函数(我还没弄明白为什么)。。积性函数满足这样一个性质
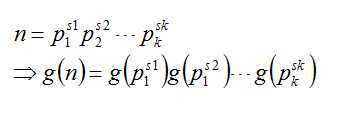
这样我们计算每个质因数即可。现在我们计算g(ps)
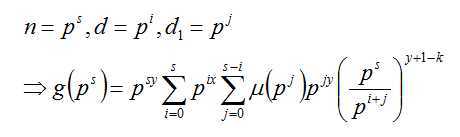
我们发现
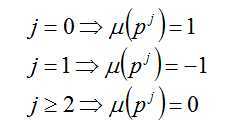
所以
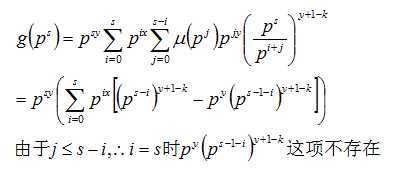
这样我们就计算出上面的B,即
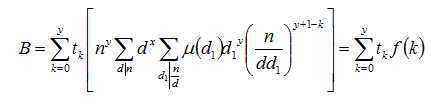
那么还剩A,我们发现A=f(1)。
这样就全部搞定。这道题涉及组合数、伯努利数以及大素数的判定分解。
const i64 mod=1000000007;
const int N=3005;
i64 exGcd(i64 a,i64 b,i64 &x,i64 &y)
{
i64 r,t;
if(b==0)
{
x=1;
y=0;
return a;
}
r=exGcd(b,a%b,x,y);
t=x;
x=y;
y=t-a/b*y;
return r;
}
i64 reverse(i64 a,i64 b)
{
i64 x,y;
exGcd(a,b,x,y);
if(x<0) x+=mod;
return x;
}
int C[N][N],p[N],pInv[N],B[N],T[N][N];
int prime[N],primeNum,tag[N];
void init()
{
p[0]=pInv[0]=1;
for(int i=1;i<N;i++)
{
p[i]=(i64)p[i-1]*i%mod;
pInv[i]=reverse(p[i],mod);
}
C[0][0]=1;
for(int i=1;i<N;i++)
{
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++)
{
C[i][j]=C[i-1][j-1]+C[i-1][j];
if(C[i][j]>=mod) C[i][j]-=mod;
}
}
B[0]=1;
for(int i=1;i<N;i++)
{
B[i]=0;
for(int j=0;j<i;j++)
{
B[i]-=(i64)C[i+1][j]*B[j]%mod;
if(B[i]<0) B[i]+=mod;
}
B[i]=B[i]*reverse(C[i+1][i],mod)%mod;
}
for(int i=0;i<N;i++)
{
i64 a=reverse(i+1,mod);
for(int j=0;j<=i;j++)
{
T[i][j]=a*B[j]%mod*C[i+1][j]%mod;
}
}
for(int i=2;i<N;i++) if(!tag[i])
{
prime[primeNum++]=i;
for(int j=i+i;j<N;j+=i) tag[j]=1;
}
}
i64 Gcd(i64 x,i64 y)
{
if(!y) return x;
return Gcd(y,x%y);
}
i64 mul(i64 x,i64 y,i64 mod)
{
i64 ans=0;
while(y)
{
if(y&1)
{
ans+=x;
if(ans>=mod) ans-=mod;
}
x<<=1;
if(x>=mod) x-=mod;
y>>=1;
}
return ans;
}
i64 myPow(i64 a,i64 b,i64 mod)
{
i64 ans=1;
while(b)
{
if(b&1) ans=mul(ans,a,mod);
a=mul(a,a,mod);
b>>=1;
}
return ans;
}
i64 myPow(i64 a,i64 b)
{
a%=mod;
i64 ans=1;
while(b)
{
if(b&1)
{
ans*=a;
if(ans>=mod) ans%=mod;
}
a*=a;
if(a>=mod) a%=mod;
b>>=1;
}
return ans;
}
void cal1(i64 n,int x,int y)
{
if(0==x)
{
printf("%lld\n",n%mod);
return;
}
i64 ans=0,p=(n+1)%mod,tmp=p;
for(int i=y;i>=0;i--)
{
ans+=T[y][i]*tmp;
ans%=mod;
tmp=tmp*p%mod;
}
ans=ans*myPow(n,y)%mod;
if(ans<0) ans+=mod;
printf("%lld\n",ans);
}
i64 all[N];
int allNum;
int witness(i64 a,i64 n)
{
i64 m=n-1,x,y,k=0;
while(!(m&1)) k++,m>>=1;
x=myPow(a,m,n);
while(k--)
{
y=mul(x,x,n);
if(1==y&&x!=1&&x!=n-1) return 1;
x=y;
}
return y!=1;
}
int isPrime(i64 n)
{
if(2==n) return 1;
if(!(n&1)) return 0;
if(1==n) return 0;
int cnt=17;
while(cnt--)
{
i64 a=rand()%(n-1)+1;
if(witness(a,n)) return 0;
}
return 1;
}
i64 pollard(i64 n,int c)
{
i64 x=1,y=1,d,k=2,i=1;
while(1)
{
x=mul(x,x,n)+c;
d=Gcd(abs(y-x),n);
if(d>1&&d<n) return d;
if(y==x) return n;
if(++i==k) y=x,k<<=1;
}
}
void split(i64 n)
{
if(1==n) return;
if(isPrime(n))
{
all[++allNum]=n;
return;
}
i64 m=n;
int c=1;
while(m==n) m=pollard(m,++c);
split(m);
split(n/m);
}
struct node
{
int primeNum;
i64 p[N];
int num[N];
i64 po[N];
}A;
i64 pw[100][100],pw1[100];
i64 get(i64 i,int y)
{
i64 tmp=1;
for(int j=1;j<=A.primeNum;j++)
{
i64 S1=0,S2=0;
i64 a=myPow(A.p[j],y);
i64 b=myPow(A.p[j],y+1-i);
pw1[0]=1;
for(int k=1;k<=A.num[j];k++)
{
pw1[k]=pw1[k-1]*b;
if(pw1[k]>=mod) pw1[k]%=mod;
}
for(int k=0;k<=A.num[j];k++)
{
S1+=pw[j][k]*pw1[A.num[j]-k];
if(S1>=mod) S1%=mod;
}
for(int k=0;k<A.num[j];k++)
{
S2+=pw[j][k]*pw1[A.num[j]-k-1]%mod*a;
if(S2>=mod) S2%=mod;
}
S1-=S2;
S1%=mod;
if(S1<0) S1+=mod;
tmp=tmp*S1;
if(tmp>=mod) tmp%=mod;
tmp=tmp*myPow(A.po[j],y);
if(tmp>=mod) tmp%=mod;
}
return tmp;
}
void cal2(i64 n,int x,int y)
{
allNum=0;
for(int i=0;i<primeNum;i++)
{
while(0==n%prime[i])
{
all[++allNum]=prime[i];
n/=prime[i];
}
}
if(n>1) split(n);
sort(all+1,all+allNum+1);
A.primeNum=1;
A.p[1]=all[1];
A.num[1]=1;
A.po[1]=all[1];
for(int i=2;i<=allNum;i++)
{
if(all[i]==all[i-1])
{
A.num[A.primeNum]++;
A.po[A.primeNum]*=all[i];
}
else
{
A.primeNum++;
A.p[A.primeNum]=all[i];
A.num[A.primeNum]=1;
A.po[A.primeNum]=all[i];
}
}
for(int i=1;i<=A.primeNum;i++)
{
pw[i][0]=1;
i64 a=myPow(A.p[i],x);
for(int j=1;j<=A.num[i];j++)
{
pw[i][j]=pw[i][j-1]*a;
if(pw[i][j]>=mod) pw[i][j]%=mod;
}
}
i64 ans=0;
for(int i=0;i<=y;i++)
{
ans+=get(i,y)*T[y][i];
ans%=mod;
}
if(y>0) ans+=get(1,y),ans%=mod;
if(ans<0) ans+=mod;
printf("%lld\n",ans);
}
int main()
{
init();
int T=myInt();
while(T--)
{
i64 n;
int x,y;
scanf("%lld%d%d",&n,&x,&y);
if(x==y) cal1(n,x,y);
else cal2(n,x,y);
}
}
标签:
原文地址:http://www.cnblogs.com/jianglangcaijin/p/4213884.html