ural 1119 Metro dp水

1119. Metro

Many of SKB Kontur programmers like to get to work by Metro because the main office is situated quite close the station Uralmash. So, since a sedentary life requires active exercises off-duty, many of the staff — Nikifor among them — walk from their homes to Metro stations on foot.

Nikifor lives in a part of our city where streets form a grid of residential quarters. All the quarters are squares with side 100 meters. A Metro entrance is situated at one of the crossroads. Nikifor starts his way from another crossroad which is south and west of the Metro entrance. Naturally, Nikifor, starting from his home, walks along the streets leading either to the north or to the east. On his way he may cross some quarters diagonally from their south-western corners to the north-eastern ones. Thus, some of the routes are shorter than others. Nikifor wonders, how long is the shortest route.

You are to write a program that will calculate the length of the shortest route from the south-western corner of the grid to the north-eastern one.

Input

There are two integers in the first line: N and M (0 < N,M ≤ 1000) — west-east and south-north sizes of the grid. Nikifor starts his way from a crossroad which is situated south-west of the quarter with coordinates (1, 1). A Metro station is situated north-east of the quarter with coordinates (N, M). The second input line contains a number K (0 ≤ K ≤ 100) which is a number of quarters that can be crossed diagonally. Then K lines with pairs of numbers separated with a space follow — these are the coordinates of those quarters.

Output

Your program is to output a length of the shortest route from Nikifor‘s home to the Metro station in meters, rounded to the integer amount of meters.

Sample

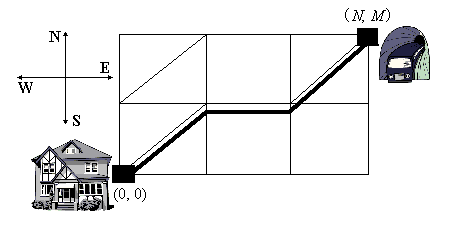
input	output
3 2 3 1 1 3 2 1 2	383

Problem Author: Leonid Volkov
Problem Source: USU Open Collegiate Programming Contest October‘2001 Junior Session

//0.156	8 110 KB
#include<stdio.h>
#include<algorithm>
#include<math.h>
#define P sqrt(2)
using namespace std;
double dp[1007][1007];
struct N
{
    int x,y;
}p[107];
int cmp(N a,N b)
{
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m)!=EOF)
	{
	    n++;m++;
        int k;
        scanf("%d",&k);
        for(int i=0;i<k;i++)
            scanf("%d%d",&p[i].x,&p[i].y);
        sort(p,p+k,cmp);
        dp[1][1]=0;
        for(int i=2;i<=n;i++)//初始化第一行
            dp[i][1]=dp[i-1][1]+1;
        for(int i=2;i<=m;i++)//初始化第一列
            dp[1][i]=dp[1][i-1]+1;
        for(int i=2;i<=n;i++)
            for(int j=2;j<=m;j++)
            {
                int flag=0;
                for(int a=0;a<k;a++)
                    if(p[a].x==(i-1)&&p[a].y==(j-1))//从三个方向得来
                        {dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+P));flag=1;break;}
                    else if(p[a].x>(i-1))break;
                if(!flag)dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//从两个方向得来
            }
        printf("%.lf\n",dp[n][m]*100);
	}
	return 0;
}