标签:
背景
之前所讨论的SVM都是非常严格的hard版本,必须要求每个点都被正确的区分开。但是,实际情况时很少出现这种情况的,因为噪声数据时无法避免的。所以,需要在hard SVM上添加容错机制,使得可以容忍少量噪声数据。
?
"软"化问题
软化SVM的思路有点类似正规化,在目标函数添加错误累加项,然后加一个系数,控制对错误的容忍度,并且在约束中添加错误容忍度的约束,形式如下:
?
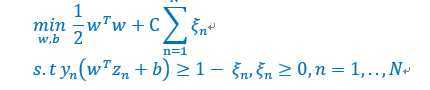
现在问题就变成了(d+1+N)个变量和2N个约束。ξ用来描述错误的容忍度。C是常量,用来控制容忍度。C越大,由于min的作用,ξ错误就会变小,也就是对错误的容忍度变小,约束变苛刻,边界变窄;反之,容忍度越大,约束变宽松,边界变宽。
?
遇到老熟人
现在,将上面软化后的SVM问题进行对偶转化和简化,得到的结果和之前hard版本十分类似,好像遇到了老熟人。
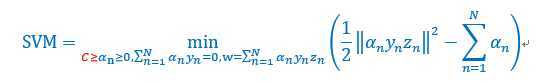
区别部分用红色高亮了,你会发现只多了N个约束。
?
α的妙用
α仍然可以使用QP方法计算得到,b的求解也是通过complementary slackness,但是在求解b的过程,可以将向量分为三类,很有参考意义,可用于数据分析。
首先看看complementary slackness条件,
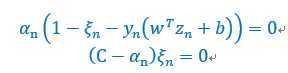
当时,向量在边界上或远离边界;
当时,,向量在边界上,称之为free支持向量;
当时,向量在边界上()或者破坏约束()。

?
具体可以参考下图,

?
SVM实战
之前4篇学习笔记,公式理论推导了一大串,感觉有点飘,那么接下来就实战SVM,这样才踏实。使用的libsvm,但是在R中调用,需要‘e1071‘扩展(install.package(‘e1071‘))。试验数据见这里。直接来代码:
library(e1071) load(‘data/train.RData‘) train$digit <- sapply(old_train_digit, function(digit) ifelse(digit == ‘0‘,‘0‘,‘non-0‘) ) train$digit <- factor(train$digit) ? m_svm <- svm(digit~., data = train, scale = FALSE, kernel = ‘radial‘, cost = 1, gamma = 100) summary(m_svm) attributes(m_svm) |
上面使用了RBF kernel,取C = 1。得到的结果中,有个属性是coefs,之前对这个属性很不了解,但是查看帮助,原文"The corresponding coefficients times the training labels",发现原来就是下面的值,
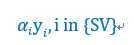
所以,如果使用线性kernel(也就是不用kernel),可以根据w的公式(如下)很方便的计算出w,
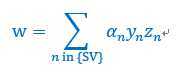
如果想实践QP,推荐使用R扩展包kernlab中的ipop函数。
?
最后,要感谢台湾大学林轩田老师设计出这么好的课程和作业,加深了我对SVM的理解,希望后面可以灵活的应用到实际工作中!
标签:
原文地址:http://www.cnblogs.com/bourneli/p/4216750.html