假设有棵树,长下面这个样子,它的前序遍历,中序遍历,后续遍历都很容易知道。
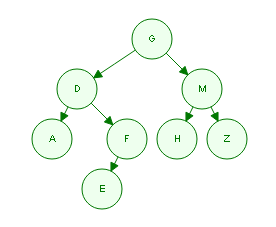
PreOrder: GDAFEMHZ
InOrder: ADEFGHMZ
PostOrder: AEFDHZMG
现在,假设仅仅知道前序和中序遍历,如何求后序遍历呢?比如,已知一棵树的前序遍历是”GDAFEMHZ”,而中序遍历是”ADEFGHMZ”应该如何求后续遍历?
第一步,root最简单,前序遍历的第一节点G就是root。
第二步,继续观察前序遍历GDAFEMHZ,除了知道G是root,剩下的节点必然是root的左右子树之外,没法找到更多信息了。
第三步,那就观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树,G右侧的HMZ必然是root的右子树。
第四步,观察左子树ADEF,左子树的中的根节点必然是大树的root的leftchild。在前序遍历中,大树的root的leftchild位于root之后,所以左子树的根节点为D。
第五步,同样的道理,root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中,一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树,并且遍历的右子树的第一个节点就是右子树的根节点。
如何知道哪里是前序遍历中的左子树和右子树的分界线呢?通过中序遍历去数节点的个数。
在上一次中序遍历中,root左侧是A、D、E、F,所以有4个节点位于root左侧。那么在前序遍历中,必然是第1个是G,第2到第5个由A、D、E、F过程,第6个就是root的右子树的根节点了,是M。
第六步,观察发现,上面的过程是递归的。先找到当前树的根节点,然后划分为左子树,右子树,然后进入左子树重复上面的过程,然后进入右子树重复上面的过程。最后就可以还原一棵树了。
第七步,其实,如果仅仅要求写后续遍历,甚至不要专门占用空间保存还原后的树。只需要稍微改动第六步,就能实现要求。仅需要把第六步的递归的过程改动为如下:
1 确定根,确定左子树,确定右子树。
2 在左子树中递归。
3 在右子树中递归。
// size是这棵树的节点个数
BinTree* CreateBinTree(char* pre,char* inorder,int size)
{
if( size == 0)
return NULL;
BinTree* root = new BinTree;
root->left = NULL;
root->right = NULL;
root->value = pre[0];
int i;
for(i= 0;i<size;i++)
if(inorder[i] == pre[0])
break;
root->left = CreateBinTree(pre+1,inorder,i);
root->right = CreateBinTree(pre+1+i,inorder+i+1,size-i-1);
return root;
}
int main()
{
char pre[]="ABDGCEFH";
char inorder[]="DGBAECHF";
BinTree* root = CreateBinTree(pre,inorder,8);
Postorder(root);
return 0;
}struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char elem;
};
void BinaryTreeFromOrderings(char* inorder, char* preorder, int length)
{
if(length == 0)
{
//cout<<"invalid length";
return;
}
TreeNode* node = new TreeNode;//Noice that [new] should be written out.
node->elem = *preorder;
int rootIndex = 0;
for(;rootIndex < length; rootIndex++)
{
if(inorder[rootIndex] == *preorder)
break;
}
//Left
BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);
//Right
BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
cout<<node->elem<<endl;
delete node;
return;
}
int main(int argc, char* argv[])
{
printf("Hello World!\n");
char* pr="GDAFEMHZ";
char* in="ADEFGHMZ";
BinaryTreeFromOrderings(in, pr, 8);
printf("\n");
return 0;
}
#include <stdio.h>
#include <stdio.h>
#include <iostream>
using namespace std;
struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char elem;
};
void BinaryTreeFromOrderings(char* inorder, char* preorder, int length)
{
if(length == 0)
{
//cout<<"invalid length";
return;
}
char node_value = *preorder;
int rootIndex = 0;
for(;rootIndex < length; rootIndex++)
{
if(inorder[rootIndex] == *preorder)
break;
}
//Left
BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);
//Right
BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
cout<<node_value<<endl;
return;
}
int main(int argc, char* argv[])
{
printf("Hello World!\n");
char* pr="GDAFEMHZ";
char* in="ADEFGHMZ";
BinaryTreeFromOrderings(in, pr, 8);
printf("\n");
return 0;
}
原文地址:http://blog.csdn.net/yusiguyuan/article/details/42687365