半变异函数/协方差建模是空间描述和空间预测之间的关键步骤。地统计的主要应用是预测未采样位置处的属性值(克里金法)。
经验半变异函数和协方差可提供有关数据集的空间自相关的信息。但是,不提供所有可能方向和距离的信息。因此,为确保克里金法预测的克里金法方差为正值,根据经验半变异函数/协方差拟合模型(即连续函数或曲线)是很有必要的。
经验半变异函数/协方差值的不同视图
地统计向导可提供经验半变异函数值的三种不同视图。可以使用任意数量(一个、两个或全部三个)的视图来帮助您根据数据拟合模型。默认视图显示了已丢弃和已平均化的经验半变异函数/协方差值。

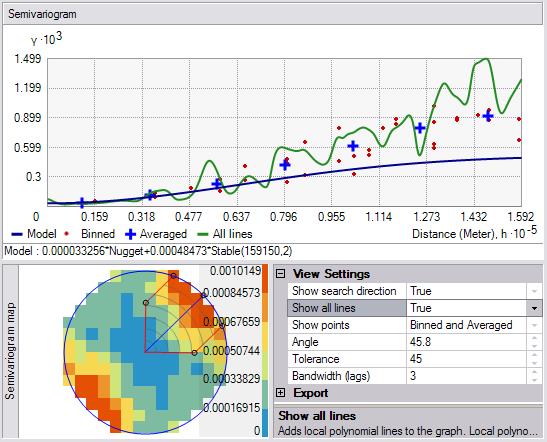
已丢弃值显示为红色的点,是通过使用宽为一个步长的方形像元将经验半变异函数/协方差点组合(分组)在一起后生成的。平均点显示为蓝色的十字符号,是通过将处于圆周分区内的经验半变异函数/协方差点进行分组后生成的。丢弃点显示半变异函数/协方差值中的局部变化,而平均值显示半变异函数/协方差值的平滑变化。在很多情况下,根据平均值拟合模型会更容易一些,因为它们将为数据中的空间自相关提供相对简洁的视图,与丢弃点相比,平均值将显示的半变异函数值的变化更为平滑。
显示点控件可以设置为“已丢弃和已平均化”(如上图所示)、“已丢弃”或“已平均化”(如下图所示)。


此外,还可以向图中添加线。这些线是根据已丢弃的经验半变异函数/协方差值进行拟合的局部多项式。如果将显示搜索方向选项设置为 True,则只会显示根据“显示搜索方向”工具的中轴样带中经验半变异函数/协方差表面拟合的局部多项式,如下图所示:
根据经验数据拟合的半变异函数/协方差模型应该:
请记住,即使模型没有完全拟合经验数据,您对现象的认识也可以决定模型的形状和块金以及变程值、偏基台值和各向异性值(回想一下,经验数据只是要构建的真实现象模型的样本,并不能完全代表真实现象的所有空间和统计方面)。
不同类型的半变异函数/协方差模型
Geostatistical Analyst 为构建经验半变异函数模型提供以下函数:
所选模型会影响未知值的预测,尤其是当接近原点的曲线形状明显不同时。接近原点处的曲线越陡,最接近的相邻元素对预测的影响就越大。
这样,输出曲面将更不平滑。每个模型都用于更准确地拟合不同种类的现象。
下图显示了两个常用模型(“指数”和“高斯”)并标识了函数的不同之处:


原文地址:http://blog.csdn.net/dsac1/article/details/42708133