标签:sgu
题目大意:
给你r1,r2,表示两个无限长的圆柱体的半径,然后这两个圆柱体的中心线相互垂直,求重复的体积。
解题思路:
这题一开始准备直接暴力积分做,然后滚粗了,不是挂精度就是wa了,所以后来就膜拜大神的做法去了,大神用的是自适应辛普森,当这个函数的(a,b)段接近二次函数的时候,这一段的积分就是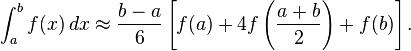 ,然后我想这道题不就是近似二次函数吗(也可能是我搞错了),然后就直接对(0,MIN(
r1 ,r2 ))用了这个公式,然后滚粗了,后来问了一个大神,他说需要有一个判断条件(假设G(l,r)代表的就是上述式子) 必须有fabs(G(l,r)-G(l,(l+r)/2)-G((l+r)/2,r))<=EPS(EPS请自己定义),这个式子公式才比较准确。然后用了一下,果然AC了。
,然后我想这道题不就是近似二次函数吗(也可能是我搞错了),然后就直接对(0,MIN(
r1 ,r2 ))用了这个公式,然后滚粗了,后来问了一个大神,他说需要有一个判断条件(假设G(l,r)代表的就是上述式子) 必须有fabs(G(l,r)-G(l,(l+r)/2)-G((l+r)/2,r))<=EPS(EPS请自己定义),这个式子公式才比较准确。然后用了一下,果然AC了。
AC代码:
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#define MIN(a,b) ((a)>(b)?(b):(a))
#define G(a,b) ((F(a)+F(b)+F((a+b)/2)*4)*(b-a)/6)
using namespace std;
double r1,r2;
double RM;
const double EPS=1e-7;
double ans=0;
inline double F(double x)
{return sqrt((r1*r1-x*x)*(r2*r2-x*x));}
inline void Count(double l,double r)
{
if(fabs(G(l,r)-G(l,(l+r)/2)-G((l+r)/2,r))<=EPS)
ans+=G(l,r)*8;
else
{
Count(l,(l+r)/2);
Count((l+r)/2,r);
}
return;
}
int main()
{
cin>>r1>>r2;
RM=MIN(r1,r2);
Count(0,RM);
printf("%lf\n",ans);
return 0;
}标签:sgu
原文地址:http://blog.csdn.net/qq_21995319/article/details/42775943