标签：

题目大意：给你n个点，拿走k个之后，让你求出怎么拿使得剩下的inertia最小。

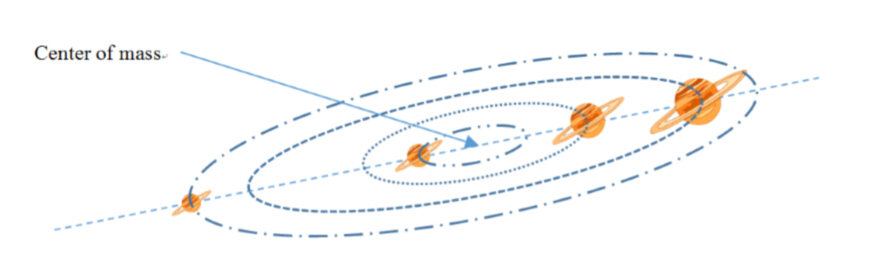
解体思路：贪心的策略。剩下的数只有当连续的时候，值会最小，枚举一遍求出来间距为n-k的最小的inertia。

PS：(x1-d)^2+(x2-d)^2+……+(xn-d)^2 = sum(x1^2+……+xn^2)+n*d*d-2*n(sum(x1+x2+……+xn)).

Galaxy

Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.


To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.

Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.

The moment of inertia I of a set of n stars can be calculated with the formula


where w_i is the weight of star i, d_i is the distance form star i to the mass of center.

As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.

Now, you are supposed to calculate the minimum moment of inertia after transportation.

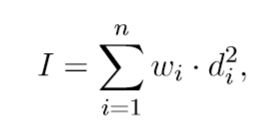
2
3 2
-1 0 1
4 2
-2 -1 1 2

0
0.5

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
///#define LL __int64
#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)
#define mod 1000000007

using namespace std;

const int maxn = 50110;

double sum1[maxn], sum2[maxn];
double num[maxn];

int main()
{
    int T;
    cin >>T;
    while(T--)
    {
        int n, k;
        cin >>n>>k;
        for(int i = 1; i <= n; i++) scanf("%lf",&num[i]);
        sort(num+1, num+1+n);
        memset(sum1, 0, sizeof(sum1));
        memset(sum2, 0, sizeof(sum2));
        int m = n-k;
        if(!m)
        {
            printf("0.0000000000\n");
            continue;
        }
        double Min = 1000000000000000000.0;
        for(int i = 1; i <= n; i++)
        {
            sum1[i] = sum1[i-1]+num[i];
            sum2[i] = sum2[i-1]+num[i]*num[i];
        }
        for(int i = 1; i <= n-m+1; i++)
        {
            int x = i;
            int y = i+m-1;
            double d = (sum1[y]-sum1[x-1])/m*1.0;
            double tmp = (sum2[y]-sum2[x-1]) + m*1.0*d*d-2.0*d*(sum1[y]-sum1[x-1]);
            Min = min(Min, tmp);
        }
        printf("%.10lf\n",Min);
    }
}

HDU 5073 Galaxy(贪心)

标签：

原文地址：http://blog.csdn.net/xu12110501127/article/details/42781825