标签：hdu2073

无限的路

甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：



甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。

5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5

1.000
2.414
10.646
54985.047
0.000

#include <stdio.h>
#include <string.h>
#include <math.h>

double cnt_b2t[210];

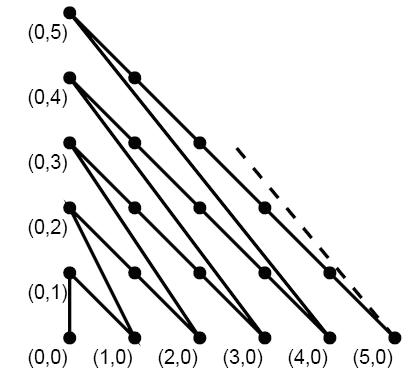
double f(int x, int y) {
	int a = x + y;
	if (!a) return 0.0;
	return cnt_b2t[a-1] + (a * (a - 1) / 2 + x) * sqrt(2.0);
}

int main() {
	freopen("stdin.txt", "r", stdin);
	int T, x1, y1, x2, y2, i;
	for (i = cnt_b2t[0] = 1; i <= 200; ++i) {
		cnt_b2t[i] = cnt_b2t[i-1] + sqrt(i*i + (i+1)*(i+1)); 
	}
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		printf("%.3lf\n", fabs(f(x1, y1) - f(x2, y2)));
	}
	return 0;
}

HDU2073 无限的路

标签：hdu2073

原文地址：http://blog.csdn.net/chang_mu/article/details/42837063