哈夫曼树与编码译码实现

时间：2015-01-19 20:32:41 阅读：608 评论：0 收藏：0 [点我收藏+]

标签：

一、哈弗曼树的基本概念。

哈夫曼树，又称最优树，是一类带权路径长度最短的树。下面有几个概念：

（1）路径。

树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

（2）路径长度。

路径上的分枝数目。

（3）树的路径长度。

从树根到每一个结点的路径长度之和。

（4）结点的带权路径长度。

从该结点到树根之间的路径长度与结点上权的乘积。

（5）树的带权路径长度。

树中所有叶子节点的带权路径长度之和。通常记作：

技术分享

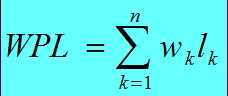
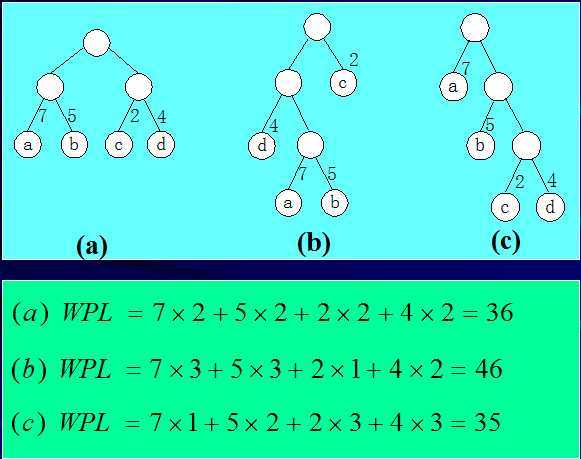
带权路径长度WPL最小的二叉树叫做最优二叉树或哈夫曼树。

二、构造哈夫曼树。

采用哈夫曼法算法构造过程为：

（1）根据给定的n个权值{w1,w2,…,wn}构成n棵二叉树的集合F={T1,T2,…,Tn},其中每棵树Ti中只有一个带权为wi的根结点，其左右子树均空。

（2）在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。

（3）在F中删除这两棵树，同时将新得到的二叉树加入到F中。

（4）重复（2）和（3），直到F只含一棵树为止。

例如权值为7,5,2,4的结点构造过程为：

技术分享

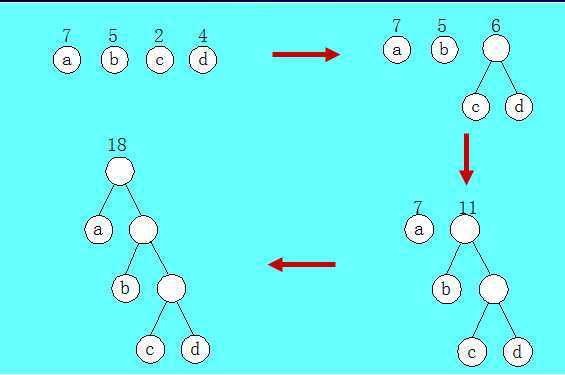
三、编码和编码树。

1、等长编码和不等长编码。

（1）等长编码。

每个字符的编码长度相同（每个编码所含的二进制位数相同）。特点是编（译）码容易，抗干扰能力强，但长度不是最短，效率低。

（2）不等长编码。

与等长编码相对，效率高。若要设计长短不等的编码（考虑译码唯一性），则必须是任一个字符的编码都不是另一个字符的编码的前缀，这种编码称作前缀编码。

2、哈夫曼编码。

考虑利用二叉树来设计二进制的前缀编码。约定左分支表示字符0，右分支表示字符1，从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码，可以证明得到的必为二进制前缀码。

考虑如何得到使电文长度最短的二进制前缀编码。可以看出，设计电文总长最短的二进制前缀编码即以n种字符出现的频率作权，构造一颗哈夫曼树。

下面给出C++参考代码：

  1 #include <iostream>
  2 #include <vector>
  3 #include <string>
  4 #include <fstream>
  5 #include <map>
  6 using namespace std;
  7 
  8 struct TNode
  9 {
 10     unsigned int weight;
 11     unsigned int parent;
 12     unsigned int lchild;
 13     unsigned int rchild;
 14     struct TNode() : weight(0), parent(0), lchild(0), rchild(0){}
 15 };
 16 
 17 class HuffTree
 18 {
 19 public:
 20     void HuffmanCode(vector<TNode> &HT, vector<string> &HC, const vector<int> &wgh);
 21     void HuffDecodeing(vector<TNode> &HT, vector<string> &HC, vector<int> &SrcCode);
 22 private:
 23     void InitHuffTree(vector<TNode> &HT, const vector<int> &wgh);
 24     void BuildHuffTree(vector<TNode> &HT, const vector<int> &wgh);
 25     void SelectTwoMin(vector<TNode> &HT, int n, int &min1, int &min2);
 26     void HuffCodeing(vector<TNode> &HT, vector<string> &HC, const vector<int> &wgh);
 27 };
 28 
 29 void HuffTree::InitHuffTree(vector<TNode> &HT, const vector<int> &wgh)
 30 {
 31     if (wgh.empty())
 32     {
 33         return;
 34     }
 35 
 36     int wghSize = wgh.size();
 37     int m = 2 * wghSize - 1;
 38     HT.resize(m + 1);
 39 
 40     for (int i = 1; i <= wghSize; ++i)
 41     {
 42         HT[i].weight = wgh[i - 1];
 43     }
 44 }
 45 
 46 void HuffTree::SelectTwoMin(vector<TNode> &HT, int n, int &min1, int &min2)
 47 {
 48     if (HT.empty())
 49     {
 50         return;
 51     }
 52 
 53     multimap<int, int> wghMap;
 54     multimap<int, int>::iterator iter;
 55     for (int i = 1; i < n; ++i)
 56     {
 57         if (HT[i].parent == 0)
 58         {
 59             wghMap.insert(make_pair(HT[i].weight, i));
 60         }
 61     }
 62 
 63     if (wghMap.size() >= 2)
 64     {
 65         iter = wghMap.begin();
 66         min1 = iter->second;
 67         min2 = (++iter)->second;
 68     }
 69 }
 70 
 71 void HuffTree::BuildHuffTree(vector<TNode> &HT, const vector<int> &wgh)
 72 {
 73     if (HT.empty() || wgh.empty())
 74     {
 75         return;
 76     }
 77 
 78     int htSize = HT.size();
 79     int wghSize = wgh.size();
 80     int wghs1, wghs2;
 81 
 82     for (int i = wghSize + 1; i < htSize; i++)
 83     {
 84         SelectTwoMin(HT, i, wghs1, wghs2);
 85 
 86         HT[wghs1].parent = i;
 87         HT[wghs2].parent = i;
 88         HT[i].lchild = wghs1;
 89         HT[i].rchild = wghs2;
 90         HT[i].weight = HT[wghs1].weight + HT[wghs2].weight;
 91     }
 92 }
 93 
 94 void HuffTree::HuffCodeing(vector<TNode> &HT, vector<string> &HC, const vector<int> &wgh)
 95 {
 96     if (HT.empty() || wgh.empty())
 97     {
 98         return;
 99     }
100 
101     int n = wgh.size() + 1;
102     int cha, par;
103     string codeTmp, code;
104 
105     for (int i = 1; i < n; i++)
106     {
107         code.clear();
108         codeTmp.clear();
109         for (cha = i, par = HT[i].parent; par != 0; cha = par, par = HT[par].parent)
110         {
111             if (HT[par].lchild == cha)
112             {
113                 codeTmp = codeTmp + "0";
114             }
115             else
116             {
117                 codeTmp = codeTmp + "1";
118             }
119         }
120 
121         for (int j = codeTmp.size() - 1; j >= 0; --j)
122         {
123             code = code + codeTmp[j];
124         }
125         HC.push_back(code);
126     }
127 }
128 
129 void HuffTree::HuffDecodeing(vector<TNode> &HT, vector<string> &HC, vector<int> &SrcCode)
130 {
131     if (HT.empty() || HC.empty())
132     {
133         return;
134     }
135 
136     string codeTmp;
137     int p, strLen;
138     for (int i = 0; i < HC.size(); ++i)
139     {
140         p = HT.size() - 1;                        //回到根结点
141         codeTmp = HC[i];
142         strLen = codeTmp.size();
143 
144         for (int j = 0; j < strLen; ++j)
145         {
146             if (codeTmp[j] == ‘0‘)
147             {
148                 p = HT[p].lchild;
149             }
150             else
151             {
152                 p = HT[p].rchild;
153             }
154         }
155         SrcCode.push_back(HT[p].weight);    
156     }
157 }    
158 
159 
160 void HuffTree::HuffmanCode(vector<TNode> &HT, vector<string> &HC, const vector<int> &wgh)
161 {
162     if (wgh.empty())
163     {
164         return;
165     }
166     InitHuffTree(HT, wgh);
167 
168     BuildHuffTree(HT, wgh);
169 
170     HuffCodeing(HT, HC, wgh);
171 }

测试部分如下：

假设源码权重为：w={5, 29, 7, 8, 14, 23, 3, 11}。文件data.txt存储源码权重值，文件Decode.txt存储编码后的结果，想要测试编码和译码结果是否一致。我的测试部分程序如下：

 1 int main(void)
 2 {
 3     ifstream chaLine("data.txt");
 4     vector<int> wgh;                            //存储权值
 5     vector<TNode> HT;                            //存储码树
 6     vector<string> HC;                            //存储编码结果
 7     HuffTree codeTree;
 8     int tmp;
 9 
10     while (chaLine >> tmp)                        /*编码测试*/
11     {
12         wgh.push_back(tmp);
13     }
14     codeTree.HuffmanCode(HT, HC, wgh);
15     for (int i = 0; i != HC.size(); ++i)
16     {
17         cout << "字符权重为: " << wgh[i] << ‘\t‘ << "编码结果为: " << HC[i] << endl;
18     }
19 
20     ifstream deLine("Decode.txt");                /*译码测试*/
21     vector<int> SrcCode;
22     string Strtmp;
23     HC.clear();
24     while (deLine >> Strtmp)
25     {
26         HC.push_back(Strtmp);
27     }
28     codeTree.HuffDecodeing(HT, HC, SrcCode);
29     for (int i = 0; i != SrcCode.size(); ++i)
30     {
31         cout << "码字:" << HC[i] << ‘\t‘ << "对应的源码权重为:"  << SrcCode[i] << endl;
32     }
33 
34     return 0;
35 }

依据测试数据建立的码树信息为：

技术分享

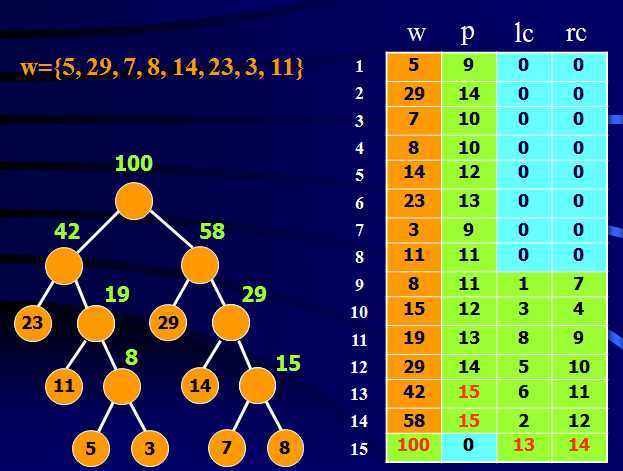
测试结果为：

技术分享

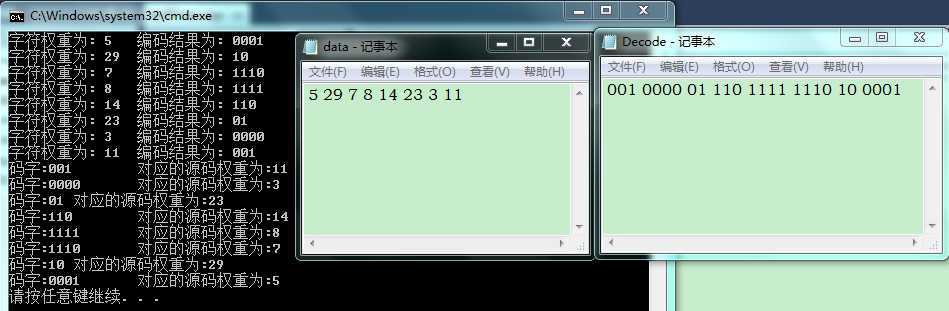
需要注意的是，建立完码树后，接下来的工作是编码（遍历码树），数据结构课本中都给出了无栈非递归遍历哈夫曼树的方法，下面的程序就是具体编码的另一种方法。

void HuffTree::HuffCodeing_1(vector<TNode> &HT, vector<string> &HC, const vector<int> &wgh)
{
    if (HT.empty() || wgh.empty())
    {
        return;
    }

    vector<TNode> HTTmp(HT);

    int p = HTTmp.size() - 1;
    string codeTmp;
    for (int i = 1; i < HTTmp.size(); ++i)
    {
        HTTmp[i].weight = 0;
    }

    while (p)
    {
        if (HTTmp[p].weight == 0)
        {
            HTTmp[p].weight += 1;
            if (HTTmp[p].lchild != 0)
            {
                p = HTTmp[p].lchild;
                codeTmp = codeTmp + "0";
            }
            else if (HTTmp[p].rchild == 0)
            {
                HC.push_back(codeTmp);
            }
        }
        else if (HTTmp[p].weight == 1)
        {
            HTTmp[p].weight += 1;
            if (HTTmp[p].rchild != 0)
            {
                p = HTTmp[p].rchild;
                codeTmp = codeTmp + "1";
            }
        }
        else
        {
            p = HTTmp[p].parent;
            if (!codeTmp.empty())
            {
                codeTmp.erase(codeTmp.size() - 1, 1);
            }
        }
    }
}

这个方法与后序遍历二叉树相似，只不过因为每个结点存储了父结点信息，所以不需要依赖栈。上面程序中定义了HTTmp局部树结构，是因为需要改变权值信息，但不能改变HT中各结点的权值信息（因为译码需要知道各个结点权值信息）。

哈夫曼树与编码译码实现

标签：

原文地址：http://www.cnblogs.com/mengwang024/p/4232962.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行