标签:
| Time Limit: 15000MS | Memory Limit: 30000K | |
| Total Submissions: 9088 | Accepted: 3472 | |
| Case Time Limit: 5000MS | ||
Description
Input
Output
Sample Input
2 6 6 5 1 4 4 6 2 2 3 6 6 4 6 5 4 3 3 6 1 6 2 6 4
Sample Output
3 4
题意简述:
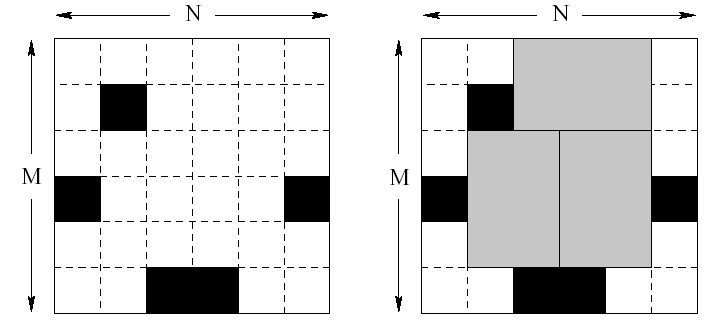
一个生产芯片的工厂要生产一种规格为2X3的芯片,方法是先产生一块规格为nXm的矩形硅片,有nXm个正方形方块组成,但是硅片上存在一些损坏的方块,显示为黑色,它们不能用来制作芯片。现在给出硅片上每个损坏方块的位置,求用该硅片最多能切割出多少块芯片。
思路:
要知道能否存在第k-2行至第k行这3行中切割出芯片及切出多少芯片,需要知道这3行上每个方块的具体状态:是否损坏,是否已经被其他芯片使用,这两种情况都称为不可用。那么可以用一个三进制数来表示某一列第k-1至第k行的状态:0表示两个方块都可用,1表示仅有第k-1行的方块可用,2表示第k行的方块不可用。
用dp[k][t]表示第k-1行至第k行所有列的三进制特征数分别等于三进制数t的每一位的状态下最多能够切割出的芯片数。那么在状态转移时,凭借上一层的状态和本层的状态就能够知道这3行的全部情况。
该题中父状态和子状态都是多对多的关系,应该对每个可行的子状态(有些状态时不可用形成的),求切割父状态并更新它的最大值。
1 #include<cstdio> 2 int map[155][15]; 3 int tri[12]={0,1,3,9,27,81,243,729,2187,6561,19683,59049}; 4 int dp[2][59049];//用滚动数组记录每一行的状态 5 int pre[15],now[15];//上一行与本行的三进制状态 6 int n,m; 7 int max(int a,int b) 8 { 9 return (a>=b)?a:b; 10 } 11 int getten(int a[])//把三进制状态转化为十进制数 12 { 13 int sum=0; 14 for(int i=1;i<=m;++i) 15 sum+=tri[i]*a[i]; 16 return sum; 17 } 18 void gettri(int k,int a[])//把十进制数转化为三进制数 19 { 20 for(int i=1;i<=m;i++) 21 { 22 a[i]=k%3; 23 k=k/3; 24 } 25 return; 26 } 27 void dfs(int i,int j,int last,int key) 28 { 29 int k; 30 dp[i%2][key]=max(dp[i%2][key],last);//不做改动,更新父状态 31 if(j>=m) 32 return; 33 if(!pre[j] && !pre[j+1] && !now[j] && !now[j+1])//竖着切割 34 { 35 now[j]=now[j+1]=2; 36 k=getten(now); 37 dfs(i,j+2,last+1,k); 38 now[j]=now[j+1]=0; 39 } 40 if(j<m-1 && !now[j] && !now[j+1] && !now[j+2]) 41 { 42 now[j]=now[j+1]=now[j+2]=2; 43 k=getten(now); 44 dfs(i,j+3,last+1,k); 45 now[j]=now[j+1]=now[j+2]=0; 46 } 47 dfs(i,j+1,last,key);//不做改动,深搜下一列 48 return; 49 } 50 int main() 51 { 52 int nn,k,a,b,tmp,ans; 53 scanf("%d",&nn); 54 while(nn--) 55 { 56 scanf("%d %d %d",&n,&m,&k); 57 for(int i=0;i<tri[m+1];++i) 58 dp[1][i]=-1;//先初始化第一行的全部状态都是不可能形成的 59 for(int i=1;i<=m;++i) 60 for(int j=1;j<=n;++j) 61 map[j][i]=0; 62 for(int i=1;i<=k;++i) 63 { 64 scanf("%d %d",&a,&b); 65 map[a][b]=1; 66 } 67 for(int i=1;i<=m;++i) 68 pre[i]=map[1][i]+1;//计算第一行的状态第0行的方块全部视为不可用 69 tmp=getten(pre); 70 dp[1][tmp]=0;//设置第一行的原本状态时可以形成的,状态值为0 71 for(int i=2;i<=n;++i)//枚举子状态 72 { 73 for(int j=0;j<tri[m+1];++j) 74 dp[i%2][j]=-1;//先设置父状态值为-1,等待更新 75 for(int j=0;j<tri[m+1];++j) 76 { 77 if(dp[(i+1)%2][j]==-1)//跳过不可能的子状态 78 continue; 79 gettri(j,pre); 80 for(int t=1;t<=m;++t) 81 { 82 if(map[i][t]) 83 now[t]=2; 84 else 85 now[t]=max(pre[t]-1,0); 86 }//根据上一行的状态得到本行的状态 87 tmp=getten(now); 88 dfs(i,1,dp[(i+1)%2][j],tmp);//深搜这一层所有可能的状态 89 } 90 } 91 ans=0; 92 for(int i=0;i<tri[m+1];++i) 93 ans=max(ans,dp[n%2][i]);//得到结果 94 printf("%d\n",ans); 95 } 96 return 0; 97 }
POJ 1038 Bugs Integrated, Inc.(状态压缩)
标签:
原文地址:http://www.cnblogs.com/caterpillarofharvard/p/4239633.html