标签:
There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
下面是O(nlgn)的解法
public class Solution { public double findMedianSortedArrays(int A[], int B[]) { int[] C = new int[A.length + B.length]; for(int i = 0; i < A.length; i++){ C[i] = A[i]; } for(int i = 0; i < B.length; i++){ C[A.length + i] = B[i]; } Arrays.sort(C); if((A.length + B.length) % 2 == 1){ return C[(A.length + B.length) / 2]; }else{ return (C[(A.length + B.length) / 2] + C[(A.length + B.length) / 2 - 1]) / 2d; } } }
还有O(m+n)的解法,两个对象指向数组开头,往后移动,直到找到第m+n/2大的。
public class Solution { public double findMedianSortedArrays(int A[], int B[]) { int i =0; int j = 0; int m = A.length; int n = B.length; double median = 0d; double last = 0d; int count = 0; while(count <= (m + n) / 2){ last = median; //如果A中的元素已经用完,直接取B数组 if(i == m){ median = B[j]; j++; }else if(j == n){//如果B中的元素已经用完,直接取A数组 median = A[i]; i++; }else if(A[i] < B[j]){ median = A[i]; i++; }else if(A[i] >= B[j]){ median = B[j]; j++; } count ++; } if((A.length + B.length) % 2 == 1){ return median; }else{ return (median + last) / 2d; } } }
最后提到的是一个极为巧妙地方法。可以在O(logm+logn)的时间内解决问题。看到时间复杂度很容易想到分治求解,可分治的模型很难确定,这里给了一个比较巧妙的思路。假定m+n为奇数,我们只要求第(m+n)/2 +1个,偶数则是求(m+n)/2 +1与(m+n)/2大数的平均数。我们令(m+n)/2+1=k。就是求A+B中第K大数的问题,只不过中位数正好是一半。
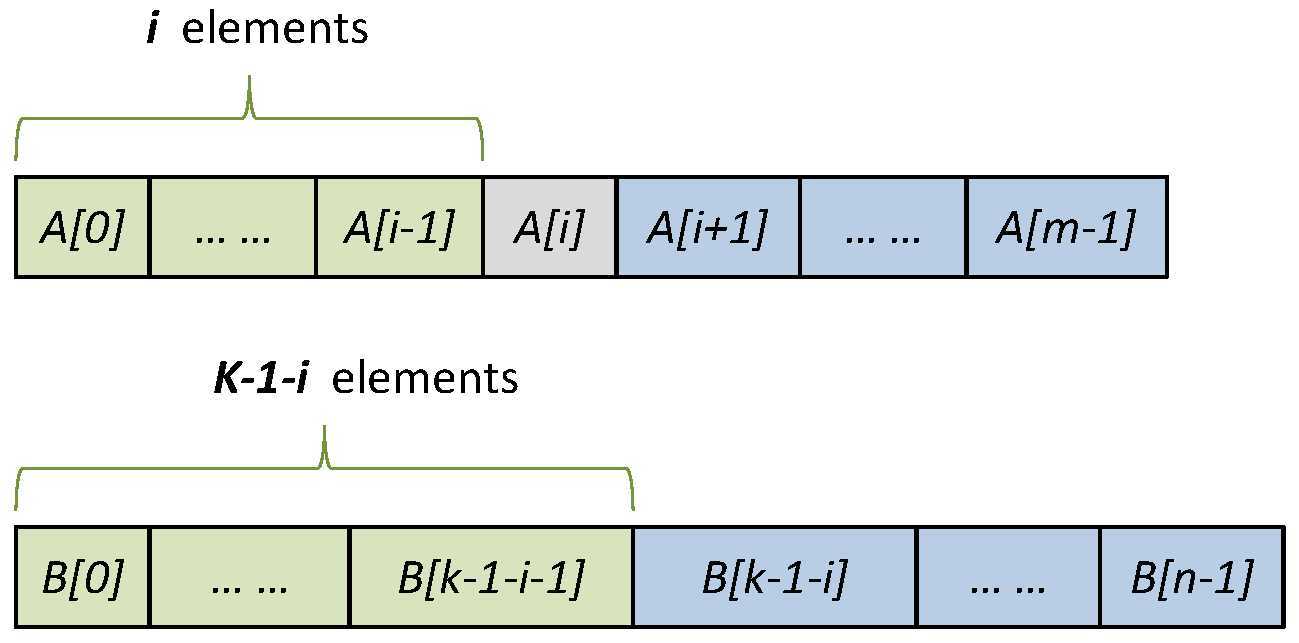
考虑在A和B中各取一半,即K/2的数字进行比较。如果这时候A[k/2- 1] < B[k/2 - 1],证明A[k/2 -1]往左的数字,都在前一半,即A[k/2 - 1]还在第k个数字之前,需要往后找。那么就把前面的舍弃,从A[k/2]开始,包括B的所有数字,寻找剩下的第k/2个。同样,如果B[k/2 - 1]大,证明这个第k大的还在B[k/2 - 1]之前,于是舍弃B[k/2 - 1]往后的数字,在剩下的中继续寻找。如此形成一个分治的解决方法。
这里要注意,如果k/2>A的元素数量,就代表A中的元素全部在第K大数字之前,全部舍去。实际上就是直接在B中找第k-m-1个了。
public class Solution { public static double findKthElement(int A[], int B[], int k){ int m = A.length; int n = B.length; //always assume that m is equal or smaller than n if(m > n){ return findKthElement(B, A, k); } if(m == 0 & n == 0){ return 0; } if(m == 0){ return B[k - 1]; } if(n == 0){ return A[k - 1]; } if (k == 1) return Math.min(A[0], B[0]); int pa = Math.min(m, k / 2); int pb = k - pa; //递归直至该条件结束 if(A[pa - 1] == B[pb - 1]){ return A[pa - 1]; }else if(A[pa - 1] < B[pb - 1]){//舍去A[pa-1]之前的元素,重新搜索第k-pa个元素 int[] C = new int[m - pa]; for(int i = 0; i < m - pa; i++){ C[i] = A[pa + i]; } return findKthElement(C, B, k - pa); }else{//舍去B[k-pb]后的元素,重新搜索第k-pb个元素 int[] C = new int[n - pb]; for(int i = 0; i < n - pb; i++){ C[i] = B[pb + i]; } return findKthElement(A, C, k - pb); } } public double findMedianSortedArrays(int A[], int B[]) { int m = A.length; int n = B.length; if((m + n) % 2 == 1){ return findKthElement(A, B, (m + n) / 2 + 1); }else{ return (findKthElement(A, B, (m + n) / 2) + findKthElement(A, B, (m + n) / 2 + 1)) / 2; } } }
标签:
原文地址:http://www.cnblogs.com/NickyYe/p/4237279.html