标签:
本题的难点在于如果用普通的办法:如递归,循环均会超时或者堆栈溢出,因此,我们需要寻找规律。
大家不妨可以先看以下代码:
#include<iostream> using namespace std; int Fiobonacci(int n) { if(n == 0) return 7; if(n == 1) return 11; return Fiobonacci(n-1) + Fiobonacci(n-2); } int main() { int fn,n; for(n = 0;n < 1000;n++) { fn = Fiobonacci(n); cout<<fn%3<<" "; if((n+1) % 8 == 0) cout<<endl; } return 0; }
运行结果为:
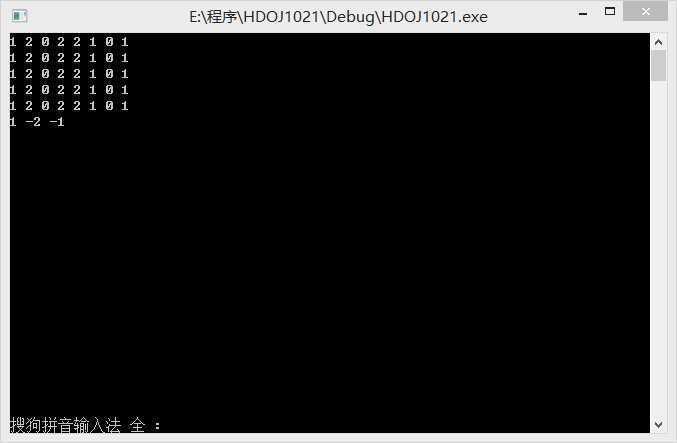
可以看出:每八个数从n=0到n=7之间f[n]%3={1,2,0,2,2,1,0,1},之后就一直按照这个规律一直下去。
但是也可以在程序运行的过程中发现程序运行越来越慢,因此根本无法满足题目的时间限制。
以下是根据这个思路设计的代码:
1 #include <stdio.h> 2 #include <stdlib.h> 3 int main(){ 4 int n; 5 int f[8]; 6 f[0]=7%3; 7 f[1]=11%3; 8 for(int i=2;i<8;i++) 9 f[i]=(f[i-1]+f[i-2])%3; 10 11 while(scanf("%d",&n)!=EOF) 12 { 13 if(f[n%8]==0) 14 printf("yes\n"); 15 else 16 printf("no\n"); 17 } 18 return 0; 19 }
标签:
原文地址:http://www.cnblogs.com/baichenjia/p/4240153.html