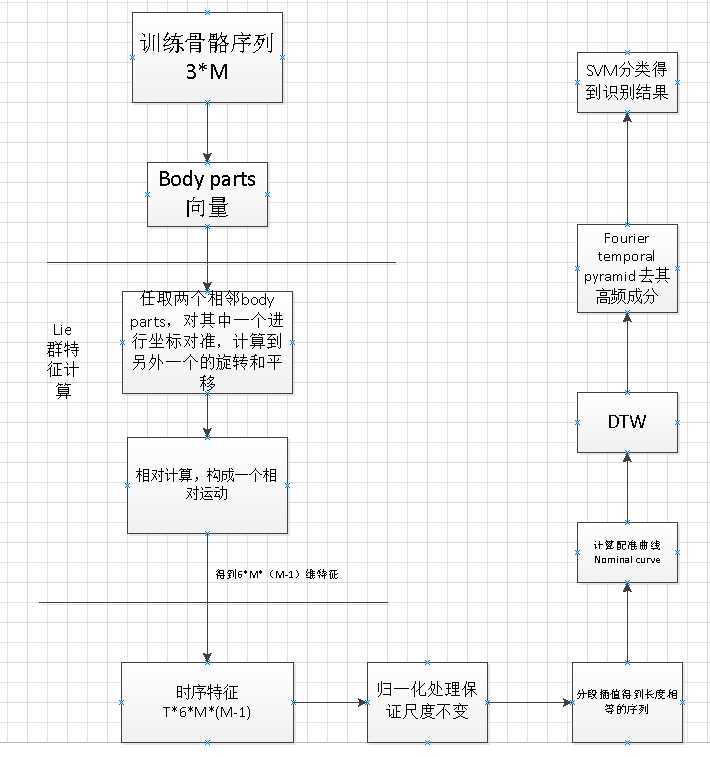
Inspired by the observation that for human actions, the relative
geometry between various body parts (though not directly connected by a
joint) provides a more meaningful description than their absolute
locations (clapping is more intuitively described using the relative
geometry between the two hands),
Given two rigid body parts, their relative geometry can be described
using the rotation and translation required to take one body part to the
position and orientation of the other
Mathematically, rigid body rotations and translations in 3D space are
members of the special Euclidean group SE(3) ,which is a matrix Lie group.
Hence, we represent the relative geometry between a pair of body parts as
a point in SE(3), and the entire human skeleton as a point in the Lie
group SE(3) � : : : � SE(3), where � denotes the direct product between
Lie groups.
With the proposed skeletal representation, human actions can be
modeled as curves (figure 1) in the Lie group SE(3) � : : : � SE(3), and
action recognition can be performed by classifying these curves. Note that
the Lie group SE(3) � : : : � SE(3) is a curved manifold and
classification of curves in this space is not a trivial task. Moreover,
standard classification approaches like SVM and temporal modeling
approaches like Fourier analysis are not directly applicable to this
curved space. To overcome these difficulties, we map the action curves
from SE(3) � : : : � SE(3) to its Lie algebra se(3) � : : : � se(3), which
is the tangent space at the identity element of the group.
To handle rate variations, for each action category, we compute a
nominal curve using dynamic time warping (DTW) , and warp all the curves
to this nominal curve. To handle the temporal misalignment and noise
issues, we represent the warped curves using the Fourier temporal pyramid
(FTP) representation
Final classification is performed using FTP and a linear SVM
classifier.
The local coordinate system of body part en is obtained by rotating
(with minimum rotation) and translating the global coordinate system such
that en1 becomes the origin and en
coincides with the x-axis (refer to figure 3(a)).