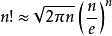
1 #include <iostream>
 2 #include <cmath>
 3 using namespace std;
 4 
 5 int main()
 6 {
 7     int n,m;
 8     double s;
 9     cin>>n;
10     while (n--)
11     {
12           s=0.0;
13           cin>>m;
14           if (m==1)
15           s=0;
16           else
17           s=(log10(2*3.141592654)*0.5+log10(m)*0.5+m*(log10(m)-log10(2.718281828459)));
18            cout <<int(s+1)<<endl;
19     }
20     return 0;
21 }