标签:
本文适合于对SVM基本概念有一点了解的童鞋。
SVM基本概念:
- 最大边缘平面——基本原理:结构风险最小化
- 分类器的泛化误差
- 支持向量
问题描述:
请对一下数据,利用svm对其进行分类。
图1
数据是这样的:看到这张图之后,发现这是一个线性可分的二分类问题。
| y=1 | 类别1 | y=-1 | 类别2 | ||
| x1 | x2 | x1 | x2 | ||
| x1 | 0 | 0 | x4 | 3 | 3 |
| x2 | 1 | 0 | x5 | 3 | 0 |
| x3 | 0 | 1 | x6 | 0 | 3 |
图2
可以看到,点XA(XA1,XA2)和点XB(XB1,XB2)在决策边界上,因此,他们符合:
w·xA+b=0
w·xB+b=0
对于任何在决策边界上方的三角形X三角形,我们可以证明:
w·x三角形+b=k == > k>0
同理,对于任何在决策边界下方的三角形X圆形,我们可以证明:
w·x圆形+b=k’ == > k’<0
因此,我们可以用以下方式预测任何测试样本z的类型:
类别1 y=1 如果w·z+b>0
类别2 y=-1 如果w·z+b<0
下面,我们来考虑一下支持向量,两个超平面可以表示如下:
bi1:w·x+b=1
bi2:w·x+b=-1
(PS:这里是一定能够表示为上面的形式,因为你可以对式子两边同时进行等倍的放大和缩小)
假设,xm和xn分别为类1和类2上的点,那么:
图3(图画的不太好,请谅解)
将xm和xn分别代入公式,则边缘d可以通过两式相减得到:
w·(x1-x2)=2 模模cosθ
||w||?d=2 可以理解为点到直线的距离
∴d=2 / ||w||
其中,||w||表示范数,这里的||w||可以理解为向量w的模(向量范数:向量x的2范数是x中各个元素平方之和再开根号),若向量w=(w1,w2),那么||w||=(w12+w22)1/2。这里,我们暂时还不知道哪些点是支持向量上的点。
SVM的训练目标就是训练出最优的W和b
让我们再来简单回顾一下:
yi=1: w·xi+b≥1
yi=-1: w·xi+b≤-1
这个条件要求,所有类别为1的训练实例(即三角形),都必须位于超平面w·x+b=1上或位于它的上方,而那些类别为2的训练实例(即圆圈)都必须位于超平面w·x+b=-1上或位于它的下方。我们可以整理出一个比较紧凑的形式:
yi(w·xi+b)≥1 , i=1,2(本例中,是二维的,故i取1和2)
尽管前面的条件可以用于其他的线性分类器,但是SVM增加了一个要求:决策边界的边缘必须是最大的。然而,最大化边缘等价于最小化下面的目标函数:
max (d=2 / ||w||) == min (||w||2 / 2)
也就是说,我们当前的目的就是
由于目标函数![]() 是二次的,而约束在参数w和b上是线性的,因此,这个问题是一个凸(convex)优化问题,可以通过标准的拉格朗日乘子法解决。
是二次的,而约束在参数w和b上是线性的,因此,这个问题是一个凸(convex)优化问题,可以通过标准的拉格朗日乘子法解决。
整理一下得到该优化问题的拉格朗日算子:
下面,根据题目,我们把具体的数据代入式子展开后得到:
因为拉格朗日乘子是未知的,因此我们仍然不能得到向量w和b的解。请仔细揣摩书上的话:
决策边界的参数w和b仅依赖于这些支持向量
也就是说,我们利用二次规划的方法可以求出在支持向量上的点的λ值(不在支持向量上的点,λ值都为0,即拉格朗日乘子都为0)。
当我们知道所有λ的值之后,根据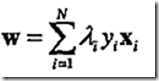 我们就可以算出w1和w2,然后在根据
我们就可以算出w1和w2,然后在根据![]() 就可以求出b的值。
就可以求出b的值。
这样,我们就圆满的完成了任务。
那么,当线性不可分的时候,我们该如何转化呢?这时就要涉及到一些更高级的东东,未完待续。
标签:
原文地址:http://www.cnblogs.com/XBWer/p/4244505.html