标签:
题目链接:http://poj.org/problem?id=3517
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 4843 | Accepted: 2576 |
Description
Let’s play a stone removing game.
Initially, n stones are arranged on a circle and numbered 1, …, n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make khops clockwise on the remaining stones and remove the one you reach. In other words, skip (k ? 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number. For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.
 Initial state |
 Step 1 |
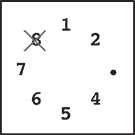 Step 2 |
 Step 3 |
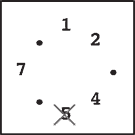 Step 4 |
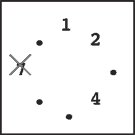 Step 5 |
 Step 6 |
 Step 7 |
 Final state |
Initial state: Eight stones are arranged on a circle.
Step 1: Stone 3 is removed since m = 3.
Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.
Step 3: You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only count stones that are still on the circle and ignore those already removed. Stone 3 is ignored in this case.
Steps 4–7: You continue until only one stone is left. Notice that in later steps when only a few stones remain, the same stone may be skipped multiple times. For example, stones 1 and 4 are skipped twice in step 7.
Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.
Input
The input consists of multiple datasets each of which is formatted as follows.
n k m
The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.
2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n
The number of datasets is less than 100.
Output
For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.
Sample Input
8 5 3 100 9999 98 10000 10000 10000 0 0 0
Sample Output
1 93 2019
Source
#include<iostream>
using namespace std;
int n,m,k;
int Ring(int cnt,int num){
int temp;
if(cnt==n){
temp=(num+m)%cnt;
if(temp)return temp;
else return cnt;
}
temp=(num+k)%cnt;
if(!temp)temp=cnt;
return Ring(cnt+1,temp);
}
int main()
{
while(cin>>n>>k>>m&&(n||m||k)){
cout<<Ring(2,1)<<endl;
}
}
#include<iostream>
#define maxn 10000+5
using namespace std;
bool round[maxn];
int n,m,k,pos,cnt;
int main()
{
cin.sync_with_stdio(false);
while(cin>>n>>k>>m&&(m||k||n)){// 8 5 3
cnt=n-1;
for(int i=0;i<n;i++)round[i]=true;
m=(m-1)%n;
round[m]=false;
pos=m;
while(cnt){
int tmpcnt=0;
while(tmpcnt!=k){
pos++;
pos%=n;
if(round[pos])tmpcnt++;
}
round[pos]=false;
cnt--;
}
cout<<pos+1<<endl;
}
return 0;
}
POJ 3517 And Then There Was One
标签:
原文地址:http://blog.csdn.net/mummyding/article/details/43062687