标签:blog class code strong color string int set cti line http
题意:n个城堡 城堡之间有路 在这n个城堡里放多少人可以防卫所有的路
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0)
描述的是这个图
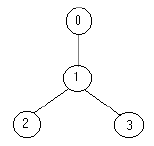
只需要在1上放一个人 就能覆盖所有的道路
zsd:
1:二分图最小点覆盖=最大匹配数
2:二分图最小顶点覆盖 = 双向二分图最大匹配 / 2 。
证明来自:www.cnbl首先,回顾一下二分图最小点覆盖的定义:
二分图中,选取最少的点数,使这些点和所有的边都有关联(把所有的边的覆盖),叫做最小点覆盖。
最少点数=最大匹配数
结合昨天看的介绍,,今天按照我的理解给出自己的证明(原创,仅作参考,欢迎讨论)
从最大匹配数到底能不能覆盖所有的边入手。
因为已知了最大匹配,所有再也不能找到增广路了,有最大匹配定义知。
现在所有的边就剩下两种情况了,一种是匹配,一种是不匹配。
假设所有的匹配边有n条,那么左右边就都有n个匹配边的顶点了,标记所有左边匹配边的顶点,则有n个。
问题就是证明n=最小点覆盖,即证明最大匹配数n到底能不能覆盖所有的边入手。
考察右边的匹配边的顶点,明显,左边都可以找到其匹配点且为n,说明所有匹配边已经被这左边的n个点关联了。
接下来证明未匹配边也能被这左边的n个匹配的点关联那么不就证明了“,使这些点和所有的边都有关联(把所有的边的覆盖)”吗。。
对于剩下的未匹配边,每条边都有一个右边点(显然既然是未匹配边,这个点自然是未匹配点)和左边点(我将证明着些左边点都是匹配边的顶点,证明了这一点,也就证明了这左边的n个点也和剩下的未匹配边关联了)
假设上面说的左边点不在这n个匹配边的左边点之中,那从剩下的某个未匹配边的右边点出发不就可以找到增广路了吗(想想增广路的定义就知道了,右未匹配,左未匹配的话那就可以找到增广路了),所以左边点也在匹配边之中,。所以就证明了剩下的未匹配边关联的范围也在这左边的n个匹配点的范围内力了。
也就证明了这n个左边匹配边的点既也右边匹配边关联,也与右边未匹配边关联了,即与所有边关联了。
那么按照最小覆盖的定义,接下来只要证明这个n是做小值就行了。
假设可以比n小,那就相当于随便删一些匹配边,那么这些删除了边的右边点就没人匹配了,也就不满足与所以边关联了,所以矛盾,所有n就是最小值。
故得证。
主要从最小覆盖的定义的两个要点(1,能不能关联所有的边。2,最小)来证明最大匹配的所有左边点就满足这个要求,匹配边有n条那自然匹配边的左边点就有n个了。
这个题太容易超时了
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 |
这个题太容易超时了<br>#include<iostream>#include<cstring>using
namespace std;int map[1501][1501];int pre[1501];int v[1501];int k,m,n;int dfs(int
j){ for(int
i=0;i<n;i++) { if(!v[i]&&map[j][i]) { v[i]=1; if(!pre[i]||dfs(pre[i])) { pre[i]=j; return
1; } } } return
0;}int
main(){ int
a,b,count,j,x; char
f; while(scanf("%d",&k)!=-1) { n=k; memset(pre,0,sizeof(pre)); memset(map,0,sizeof(map)); for(x=0;x<k;x++) { // cin>>a>>f>>f>>j>>f; scanf("%d:(%d)",&a,&j); for(int
i=1;i<=j;i++) { scanf("%d",&b); map[a][b]=1; map[b][a]=1; } } count=0; for(int
i=0;i<n;i++) { memset(v,0,sizeof(v)); if(dfs(i)) count++; } cout<<count/2<<endl; } return
0;} |
标签:blog class code strong color string int set cti line http
原文地址:http://www.cnblogs.com/zhangdashuai/p/3701442.html