标签:
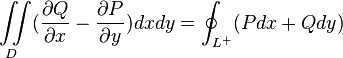
Green公式揭示了平面区域的二重积分和封闭曲线上的线积分的关系。
其中L+表示沿着封闭区域的边界曲线正向。
并且由Green公式的推导过程我们知道:
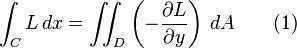
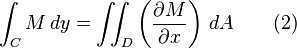
这里若L=-y,可以保证(1)式子在区域中恒正,且等于封闭区域面积。
同理,M=x,也可以保证(2)式子在区域中恒正,且等于封闭区域面积。
所以我们只需沿着多边形的边求曲线积分,若积分为正,则是沿着边界曲线正方向(逆时针),反之为顺时针,且所得绝对值为多边形面积。
NOTE:边界曲线的正向即沿着边界曲线,单连通区域总在边界曲线的左边。(这里边界曲线正向,即我们所看到的逆时针方向)
这里假设我们程序中的多边形点为(x0,y0), (x1,y1), (x2,y2), . . . (xn-1,yn-1)
我们来计算![]() 沿着点(x0,y0), (x1,y1), (x2,y2), . . . (xn-1,yn-1)的曲线积分。
沿着点(x0,y0), (x1,y1), (x2,y2), . . . (xn-1,yn-1)的曲线积分。
其中对于每段分割线段,y取( yn + yn+1) / 2 , dx=xn+1 - xn
d=0; for(int i=0;i<n-1;i++) { d+= -0.5*(y[i+1]+y[i])*(x[i+1]-x[i]); } if(d>0) std::cout<<"counter clockwise"<<std::endl; else std::cout<<"clockwise"<<std::endl;
这个方法比较简单,遍历所有点,找到x最大的点Pm(该点一定在最右端曲线的“凸起”部分上),然后取该点前后各一个点Pm-1、Pm+1,组成向量(Pm-1,Pm)、(Pm,Pm+1)。然后进行向量叉乘即可判断出顺时针或逆时针。
如图,规定向量叉乘使用“右手定则”
+表示该点Pm和前后两个点组成的两个向量(Pm-1,Pm)、(Pm,Pm+1),叉乘得到的向量指向z轴负方向;
-表示(Pm-1,Pm)x(Pm,Pm+1)得到的向量指向z轴方向。
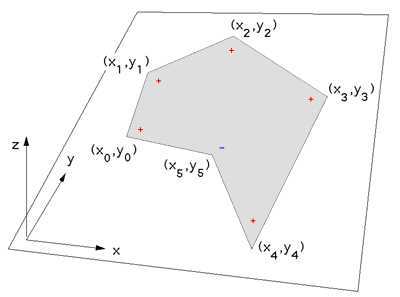
NOTE:这里必须进行遍历寻找凸点,否则若多边形含有凹的部分,并且选取的点于凹部分中,会得到相反的结果。
标签:
原文地址:http://www.cnblogs.com/kyokuhuang/p/4250526.html