POJ 1177 & HDU 1828 Picture（扫描线 + 求周长）

标签：扫描线   hdu   poj   

题目链接：

POJ:http://poj.org/problem?id=1177

HDU:http://acm.hdu.edu.cn/showproblem.php?pid=1828

几个不错的讲解：

http://www.cnblogs.com/scau20110726/archive/2013/04/13/3018702.html

http://blog.csdn.net/xingyeyongheng/article/details/8931410

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter. 

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 

The corresponding boundary is the whole set of line segments drawn in Figure 2. 

The vertices of all rectangles have integer coordinates. 

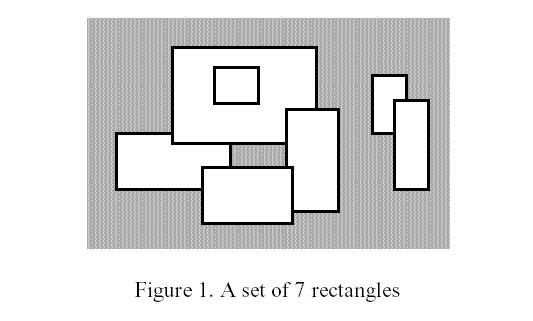
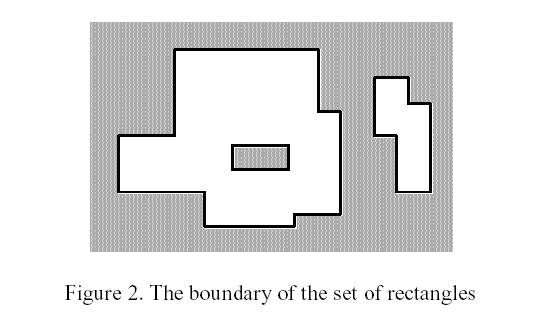
Input

Output

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Source

题目链接：

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
using namespace std;
#define N 5017
#define MAX 10100
#define ll root*2
#define rr root*2+1
//#define mid (a[root].l+a[root].r)>>1

struct Line
{
    int l, r;
    int h;//高度
    int flag;//若该扫描线属于矩形的下边的横边，则叫做入边，值为1，若属于矩形的上边的横边，则叫做出边，值为-1
} line[N*2];

struct node
{
    int l, r;
    int lp, rp;//是一个标记量，只有0,1，表示这个节点左右两个端点没有被覆盖，有为1，无为0
    int num;//这个区间被多少条线段覆盖
    int cover;//表示某x轴坐标区间内是否有边覆盖
    int len;//区间覆盖边长度
} a[2*MAX*4];

bool cmp(Line a,Line b)
{
    return a.h < b.h;
}

void build(int left,int right,int root)//构造线段树
{
    a[root].l = left;
    a[root].r = right;
    a[root].cover = 0;
    a[root].len = 0;
    a[root].lp = a[root].rp = a[root].num=0;
    if(left == right)
        return;
    int mid = (a[root].l+a[root].r)>>1;
    build(left,mid,ll);
    build(mid+1,right,rr);
}
void pushup(int root)
{
    if(a[root].cover)
    {
        a[root].len = a[root].r-a[root].l+1;
        a[root].lp = a[root].rp = 1;
        a[root].num = 1;
    }
    else if(a[root].l == a[root].r)//叶子
    {
        a[root].len = 0;
        a[root].lp = a[root].rp = 0;
        a[root].num = 0;
    }
    else
    {
        a[root].len = a[ll].len+a[rr].len;
        a[root].lp = a[ll].lp;
        a[root].rp = a[rr].rp;
        a[root].num = a[ll].num + a[rr].num - (a[ll].rp&a[rr].lp);
    }
}

void update(int left,int right,int val,int root)//加入线段e，后更新线段树
{
    if(left > right)
        return;
    if(a[root].l==left && a[root].r==right)//目标区间
    {
        a[root].cover+=val;//插入或删除操作直接让cover[]+=flag。当cover[]>0时，该区间一定有边覆盖。
        pushup(root);
        return;
    }
    int mid = (a[root].l+a[root].r)>>1;
    if(right <= mid)
        update(left,right,val,ll);
    else if(left > mid)
        update(left,right,val,rr);
    else
    {
        update(left,mid,val,ll);
        update(mid+1,right,val,rr);
    }
    pushup(root);
}
int main()
{
    int n, i, k;
    while(scanf("%d",&n)!=EOF)
    {
        if(n == 0)
        {
            printf("0\n");
            continue;
        }
        k = 0;
        int x1, y1, x2, y2;
        int maxx = -MAX;//方便此题建树
        int minn = MAX;
        for(i = 0; i < n; i++)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            //本题采用平行x轴的扫描线从下往上扫描
            maxx = max(maxx, x2);
            minn = min(minn, x1);
            line[k].l = x1;
            line[k].r = x2;
            line[k].h = y1;
            line[k].flag = 1;
            line[k+1].l = x1;
            line[k+1].r = x2;
            line[k+1].h = y2;
            line[k+1].flag = -1;    //把图中的边用line存起来以便排序
            k += 2;
        }
        sort(line,line+k,cmp);
        build(minn, maxx-1, 1);

        int ans = 0;
        int prelen = 0;
        line[k] = line[k+1];//每次处理循环的最后一次
        for(i = 0; i < k; i++)
        {
            update(line[i].l,line[i].r-1,line[i].flag,1);//每插入一次就算一次 ，相对应的边在线段树中会抵消
            //ans+=(line[i+1].h-line[i].h)*a[1].len;//高 X 低
            ans += abs(a[1].len - prelen); //计算横线部分
            ans += (line[i+1].h-line[i].h) * (2*a[1].num); //计算竖线部分
            prelen = a[1].len;//之前的长度
        }
        printf("%d\n",ans);
    }
    return 0;
}

POJ 1177 & HDU 1828 Picture（扫描线 + 求周长）

标签：扫描线   hdu   poj   

原文地址：http://blog.csdn.net/u012860063/article/details/43203093