标签:
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。本文作为分类算法的第一篇,将首先介绍分类问题,对分类问题进行一个正式的定义。然后,介绍贝叶斯分类算法的基础——贝叶斯定理。最后,通过实例讨论贝叶斯分类中最简单的一种:朴素贝叶斯分类。
对于分类问题,其实谁都不会陌生,说我们每个人每天都在执行分类操作一点都不夸张,只是我们没有意识到罢了。例如,当你看到一个陌生人,你的脑子下意识判断TA是男是女;你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱、那边有个非主流”之类的话,其实这就是一种分类操作。
从数学角度来说,分类问题可做如下定义:
已知集合: 和
和 ,确定映射规则
,确定映射规则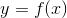 ,使得任意
,使得任意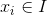 有且仅有一个
有且仅有一个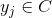 使得
使得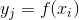 成立。(不考虑模糊数学里的模糊集情况)
成立。(不考虑模糊数学里的模糊集情况)
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合,其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
这里要着重强调,分类问题往往采用经验性方法构造映射规则,即一般情况下的分类问题缺少足够的信息来构造100%正确的映射规则,而是通过对经验数据的学习从而实现一定概率意义上正确的分类,因此所训练出的分类器并不是一定能将每个待分类项准确映射到其分类,分类器的质量与分类器构造方法、待分类数据的特性以及训练样本数量等诸多因素有关。
例如,医生对病人进行诊断就是一个典型的分类过程,任何一个医生都无法直接看到病人的病情,只能观察病人表现出的症状和各种化验检测数据来推断病情,这时医生就好比一个分类器,而这个医生诊断的准确率,与他当初受到的教育方式(构造方法)、病人的症状是否突出(待分类数据的特性)以及医生的经验多少(训练样本数量)都有密切关系。
每次提到贝叶斯定理,我心中的崇敬之情都油然而生,倒不是因为这个定理多高深,而是因为它特别有用。这个定理解决了现实生活里经常遇到的问题:已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率:
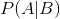 表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为: 。
。
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
下面不加证明地直接给出贝叶斯定理:
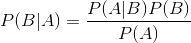
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类的正式定义如下:
1、设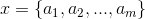 为一个待分类项,而每个a为x的一个特征属性。
为一个待分类项,而每个a为x的一个特征属性。
2、有类别集合 。
。
3、计算 。
。
4、如果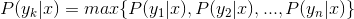 ,则
,则 。
。
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做:
1、找到一个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各类别下各个特征属性的条件概率估计。即
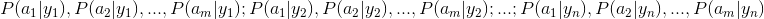 。
。
3、如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导:

因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的,所以有:

根据上述分析,朴素贝叶斯分类的流程可以由下图表示(暂时不考虑验证):
可以看到,整个朴素贝叶斯分类分为三个阶段:
第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
这一节讨论P(a|y)的估计。
由上文看出,计算各个划分的条件概率P(a|y)是朴素贝叶斯分类的关键性步骤,当特征属性为离散值时,只要很方便的统计训练样本中各个划分在每个类别中出现的频率即可用来估计P(a|y),下面重点讨论特征属性是连续值的情况。
当特征属性为连续值时,通常假定其值服从高斯分布(也称正态分布)。即:

而
因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差,代入上述公式即可得到需要的估计值。均值与标准差的计算在此不再赘述。
另一个需要讨论的问题就是当P(a|y)=0怎么办,当某个类别下某个特征项划分没有出现时,就是产生这种现象,这会令分类器质量大大降低。为了解决这个问题,我们引入Laplace校准,它的思想非常简单,就是对没类别下所有划分的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为0的尴尬局面。
下面讨论一个使用朴素贝叶斯分类解决实际问题的例子,为了简单起见,对例子中的数据做了适当的简化。
这个问题是这样的,对于SNS社区来说,不真实账号(使用虚假身份或用户的小号)是一个普遍存在的问题,作为SNS社区的运营商,希望可以检测出这些不真实账号,从而在一些运营分析报告中避免这些账号的干扰,亦可以加强对SNS社区的了解与监管。
如果通过纯人工检测,需要耗费大量的人力,效率也十分低下,如能引入自动检测机制,必将大大提升工作效率。这个问题说白了,就是要将社区中所有账号在真实账号和不真实账号两个类别上进行分类,下面我们一步一步实现这个过程。
首先设C=0表示真实账号,C=1表示不真实账号。
1、确定特征属性及划分
这一步要找出可以帮助我们区分真实账号与不真实账号的特征属性,在实际应用中,特征属性的数量是很多的,划分也会比较细致,但这里为了简单起见,我们用少量的特征属性以及较粗的划分,并对数据做了修改。
我们选择三个特征属性:a1:日志数量/注册天数,a2:好友数量/注册天数,a3:是否使用真实头像。在SNS社区中这三项都是可以直接从数据库里得到或计算出来的。
下面给出划分:a1:{a<=0.05, 0.05<a<0.2, a>=0.2},a1:{a<=0.1, 0.1<a<0.8, a>=0.8},a3:{a=0(不是),a=1(是)}。
2、获取训练样本
这里使用运维人员曾经人工检测过的1万个账号作为训练样本。
3、计算训练样本中每个类别的频率
用训练样本中真实账号和不真实账号数量分别除以一万,得到:


4、计算每个类别条件下各个特征属性划分的频率
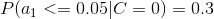






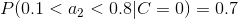

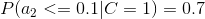

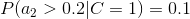

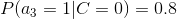


5、使用分类器进行鉴别
下面我们使用上面训练得到的分类器鉴别一个账号,这个账号使用非真实头像,日志数量与注册天数的比率为0.1,好友数与注册天数的比率为0.2。
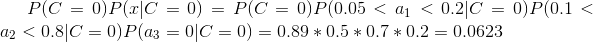
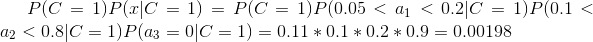
可以看到,虽然这个用户没有使用真实头像,但是通过分类器的鉴别,更倾向于将此账号归入真实账号类别。这个例子也展示了当特征属性充分多时,朴素贝叶斯分类对个别属性的抗干扰性。
虽然后续还会提到其它分类算法,不过这里我想先提一下如何评价分类器的质量。
首先要定义,分类器的正确率指分类器正确分类的项目占所有被分类项目的比率。
通常使用回归测试来评估分类器的准确率,最简单的方法是用构造完成的分类器对训练数据进行分类,然后根据结果给出正确率评估。但这不是一个好方法,因为使用训练数据作为检测数据有可能因为过分拟合而导致结果过于乐观,所以一种更好的方法是在构造初期将训练数据一分为二,用一部分构造分类器,然后用另一部分检测分类器的准确率。
在上一篇文章中我们讨论了朴素贝叶斯分类。朴素贝叶斯分类有一个限制条件,就是特征属性必须有条件独立或基本独立(实际上在现实应用中几乎不可能做到完全独立)。当这个条件成立时,朴素贝叶斯分类法的准确率是最高的,但不幸的是,现实中各个特征属性间往往并不条件独立,而是具有较强的相关性,这样就限制了朴素贝叶斯分类的能力。这一篇文章中,我们接着上一篇文章的例子,讨论贝叶斯分类中更高级、应用范围更广的一种算法——贝叶斯网络(又称贝叶斯信念网络或信念网络)。
上一篇文章我们使用朴素贝叶斯分类实现了SNS社区中不真实账号的检测。在那个解决方案中,我做了如下假设:
i、真实账号比非真实账号平均具有更大的日志密度、各大的好友密度以及更多的使用真实头像。
ii、日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的。
但是,上述第二条假设很可能并不成立。一般来说,好友密度除了与账号是否真实有关,还与是否有真实头像有关,因为真实的头像会吸引更多人加其为好友。因此,我们为了获取更准确的分类,可以将假设修改如下:
i、真实账号比非真实账号平均具有更大的日志密度、各大的好友密度以及更多的使用真实头像。
ii、日志密度与好友密度、日志密度与是否使用真实头像在账号真实性给定的条件下是独立的。
iii、使用真实头像的用户比使用非真实头像的用户平均有更大的好友密度。
上述假设更接近实际情况,但问题随之也来了,由于特征属性间存在依赖关系,使得朴素贝叶斯分类不适用了。既然这样,我去寻找另外的解决方案。
下图表示特征属性之间的关联:

上图是一个有向无环图,其中每个节点代表一个随机变量,而弧则表示两个随机变量之间的联系,表示指向结点影响被指向结点。不过仅有这个图的话,只能定性给出随机变量间的关系,如果要定量,还需要一些数据,这些数据就是每个节点对其直接前驱节点的条件概率,而没有前驱节点的节点则使用先验概率表示。
例如,通过对训练数据集的统计,得到下表(R表示账号真实性,H表示头像真实性):
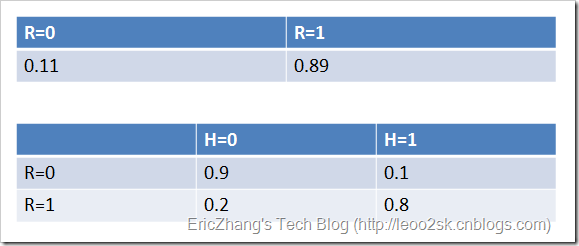
纵向表头表示条件变量,横向表头表示随机变量。上表为真实账号和非真实账号的概率,而下表为头像真实性对于账号真实性的概率。这两张表分别为“账号是否真实”和“头像是否真实”的条件概率表。有了这些数据,不但能顺向推断,还能通过贝叶斯定理进行逆向推断。例如,现随机抽取一个账户,已知其头像为假,求其账号也为假的概率:
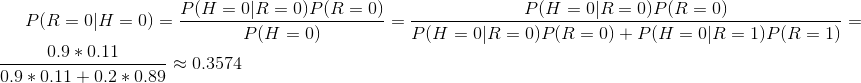
也就是说,在仅知道头像为假的情况下,有大约35.7%的概率此账户也为假。如果觉得阅读上述推导有困难,请复习概率论中的条件概率、贝叶斯定理及全概率公式。如果给出所有节点的条件概率表,则可以在观察值不完备的情况下对任意随机变量进行统计推断。上述方法就是使用了贝叶斯网络。
有了上述铺垫,我们就可以正式定义贝叶斯网络了。
一个贝叶斯网络定义包括一个有向无环图(DAG)和一个条件概率表集合。DAG中每一个节点表示一个随机变量,可以是可直接观测变量或隐藏变量,而有向边表示随机变量间的条件依赖;条件概率表中的每一个元素对应DAG中唯一的节点,存储此节点对于其所有直接前驱节点的联合条件概率。
贝叶斯网络有一条极为重要的性质,就是我们断言每一个节点在其直接前驱节点的值制定后,这个节点条件独立于其所有非直接前驱前辈节点。
这个性质很类似Markov过程。其实,贝叶斯网络可以看做是Markov链的非线性扩展。这条特性的重要意义在于明确了贝叶斯网络可以方便计算联合概率分布。一般情况先,多变量非独立联合条件概率分布有如下求取公式:

而在贝叶斯网络中,由于存在前述性质,任意随机变量组合的联合条件概率分布被化简成
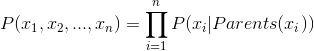
其中Parents表示xi的直接前驱节点的联合,概率值可以从相应条件概率表中查到。
贝叶斯网络比朴素贝叶斯更复杂,而想构造和训练出一个好的贝叶斯网络更是异常艰难。但是贝叶斯网络是模拟人的认知思维推理模式,用一组条件概率函数以及有向无环图对不确定性的因果推理关系建模,因此其具有更高的实用价值。
构造与训练贝叶斯网络分为以下两步:
1、确定随机变量间的拓扑关系,形成DAG。这一步通常需要领域专家完成,而想要建立一个好的拓扑结构,通常需要不断迭代和改进才可以。
2、训练贝叶斯网络。这一步也就是要完成条件概率表的构造,如果每个随机变量的值都是可以直接观察的,像我们上面的例子,那么这一步的训练是直观的,方法类似于朴素贝叶斯分类。但是通常贝叶斯网络的中存在隐藏变量节点,那么训练方法就是比较复杂,例如使用梯度下降法。由于这些内容过于晦涩以及牵扯到较深入的数学知识,在此不再赘述,有兴趣的朋友可以查阅相关文献。
贝叶斯网络作为一种不确定性的因果推理模型,其应用范围非常广,在医疗诊断、信息检索、电子技术与工业工程等诸多方面发挥重要作用,而与其相关的一些问题也是近来的热点研究课题。例如,Google就在诸多服务中使用了贝叶斯网络。
就使用方法来说,贝叶斯网络主要用于概率推理及决策,具体来说,就是在信息不完备的情况下通过可以观察随机变量推断不可观察的随机变量,并且不可观察随机变量可以多于以一个,一般初期将不可观察变量置为随机值,然后进行概率推理。下面举一个例子。
还是SNS社区中不真实账号检测的例子,我们的模型中存在四个随机变量:账号真实性R,头像真实性H,日志密度L,好友密度F。其中H,L,F是可以观察到的值,而我们最关系的R是无法直接观察的。这个问题就划归为通过H,L,F的观察值对R进行概率推理。推理过程可以如下表示:
1、使用观察值实例化H,L和F,把随机值赋给R。
2、计算 。其中相应概率值可以查条件概率表。
。其中相应概率值可以查条件概率表。
由于上述例子只有一个未知随机变量,所以不用迭代。更一般得,使用贝叶斯网络进行推理的步骤可如下描述:
1、对所有可观察随机变量节点用观察值实例化;对不可观察节点实例化为随机值。
2、对DAG进行遍历,对每一个不可观察节点y,计算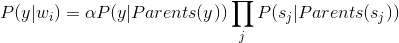 ,其中wi表示除y以外的其它所有节点,a为正规化因子,sj表示y的第j个子节点。
,其中wi表示除y以外的其它所有节点,a为正规化因子,sj表示y的第j个子节点。
3、使用第三步计算出的各个y作为未知节点的新值进行实例化,重复第二步,直到结果充分收敛。
4、将收敛结果作为推断值。
以上只是贝叶斯网络推理的算法之一,另外还有其它算法,这里不再详述。
转载:http://www.cnblogs.com/hexinuaa/articles/2143483.html
标签:
原文地址:http://my.oschina.net/u/1426212/blog/372882