标签：
一、简介：
伸展树，或者叫自适应查找树，是一种用于保存有序集合的简单高效的数据结构。伸展树实质上是一个二叉查找树。允许查找，插入，删除，删除最小，删除最大，分割，合并等许多操作，这些操作的时间复杂度为O(logN)。由于伸展树可以适应需求序列，因此他们的性能在实际应用中更优秀。
伸展树支持所有的二叉树操作。伸展树不保证最坏情况下的时间复杂度为O(logN)。伸展树的时间复杂度边界是均摊的。尽管一个单独的操作可能很耗时，但对于一个任意的操作序列，时间复杂度可以保证为O(logN)。
二、自调整和均摊分析：
平衡查找树的一些限制：
1、平衡查找树每个节点都需要保存额外的信息。
2、难于实现，因此插入和删除操作复杂度高，且是潜在的错误点。
3、对于简单的输入，性能并没有什么提高。
平衡查找树可以考虑提高性能的地方：
1、平衡查找树在最差、平均和最坏情况下的时间复杂度在本质上是相同的。
2、对一个节点的访问，如果第二次访问的时间小于第一次访问，将是非常好的事情。
3、90-10法则。在实际情况中，90%的访问发生在10%的数据上。
4、处理好那90%的情况就很好了。
三、均摊时间边界：
在一颗二叉树中访问一个节点的时间复杂度是这个节点的深度。因此，我们可以重构树的结构，使得被经常访问的节点朝树根的方向移动。尽管这会引入额外的操作，但是经常被访问的节点被移动到了靠近根的位置，因此，对于这部分节点，我们可以很快的访问。根据上面的90-10法则，这样做可以提高性能。
为了达到上面的目的，我们需要使用一种策略──旋转到根(rotate-to-root)。具体实现如下：
旋转分为左旋和右旋，这两个是对称的。图示：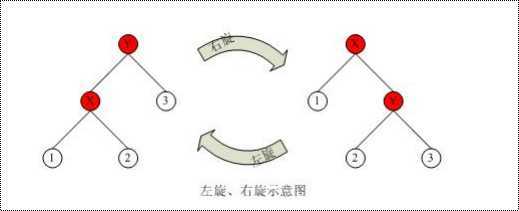 
为了叙述的方便，上图的右旋叫做X绕Y右旋，左旋叫做Y绕X左旋。 下图展示了将节点3旋转到根：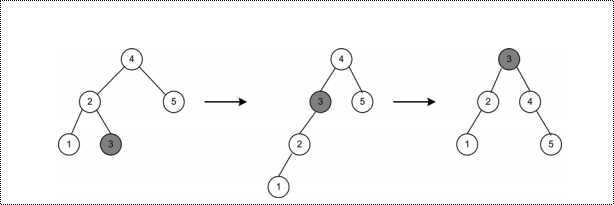 
图1
首先节点3绕2左旋，然后3绕节点4右旋。 注意：所查找的数据必须符合上面的90-10法则，否则性能上不升反降！！ 四、基本的自底向上伸展树： 应用伸展（splaying）技术，可以得到对数均摊边界的时间复杂度。 在旋转的时候，可以分为三种情况：
1、zig情况。
X是查找路径上我们需要旋转的一个非根节点。 如果X的父节点是根，那么我们用下图所示的方法旋转X到根：
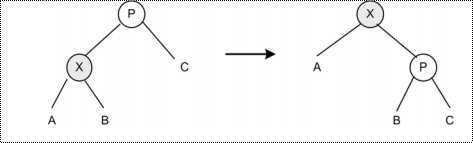
图2
这和一个普通的单旋转相同。
2、zig-zag情况。
在这种情况中，X有一个父节点P和祖父节点G（P的父节点）。X是右子节点，P是左子节点，或者反过来。这个就是双旋转。 先是X绕P左旋转，再接着X绕G右旋转。 如图所示：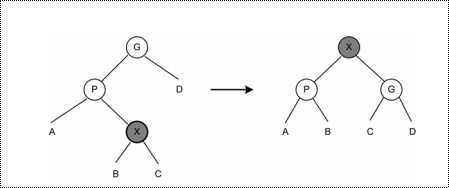 
图三
3、zig-zig情况。
这和前一个旋转不同。在这种情况中，X和P都是左子节点或右子节点。 先是P绕G右旋转，接着X绕P右旋转。 如图所示：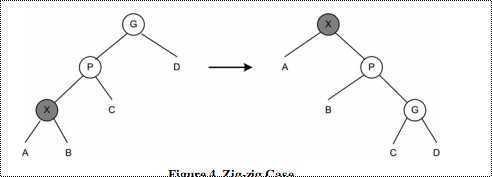 
图四
下面是splay的伪代码：
P(X) : 获得X的父节点，G(X) : 获得X的祖父节点（=P(P(X))）。
Function Buttom-up-splay:
Do
If X 是 P(X) 的左子结点 Then
If G(X) 为空 Then
X 绕 P（X）右旋
Else If P（X）是G（X）的左子结点
P(X) 绕G(X)右旋
X 绕P(X)右旋
Else
X绕P(X)右旋
X绕P(X)左旋 (P(X)和上面一句的不同，是原来的G(X))
Endif
Else If X 是 P(X) 的右子结点 Then
If G(X) 为空 Then
X 绕 P（X）左旋
Else If P（X）是G（X）的右子结点
P(X) 绕G(X)左旋
X 绕P(X)左旋
Else
X绕P(X)左旋
X绕P(X)右旋 (P(X)和上面一句的不同，是原来的G(X))
Endif
Endif
While (P(X) != NULL)
EndFunction
仔细分析zig-zag，可以发现，其实zig-zag就是两次zig。因此上面的代码可以简化：
Function Buttom-up-splay:
Do
If X 是 P(X) 的左子结点 Then
If P（X）是G（X）的左子结点
P(X) 绕G(X)右旋
Endif
X 绕P(X)右旋
Else If X 是 P(X) 的右子结点 Then
If P（X）是G（X）的右子结点
P(X) 绕G(X)左旋
Endif
X 绕P(X)左旋
Endif
While (P(X) != NULL)
EndFunction
下面是一个例子，旋转节点c到根上。
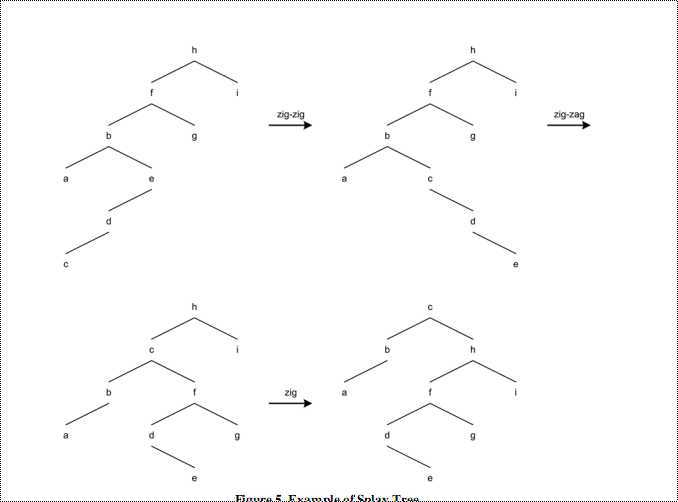图五
五、基本伸展树操作：
1、插入：
当一个节点插入时，伸展操作将执行。因此，新插入的节点在根上。
2、查找：
如果查找成功（找到），那么由于伸展操作，被查找的节点成为树的新根。
如果查找失败（没有），那么在查找遇到NULL之前的那个节点成为新的根。也就是，如果查找的节点在树中，那么，此时根上的节点就是距离这个节点最近的节点。
3、查找最大最小：
查找之后执行伸展。
4、删除最大最小：
a)删除最小：
首先执行查找最小的操作。
这时，要删除的节点就在根上。根据二叉查找树的特点，根没有左子节点。
使用根的右子结点作为新的根，删除旧的包含最小值的根。
b)删除最大：
首先执行查找最大的操作。
删除根，并把被删除的根的左子结点作为新的根。
5、删除：
将要删除的节点移至根。
删除根，剩下两个子树L（左子树）和R（右子树）。
使用DeleteMax查找L的最大节点，此时，L的根没有右子树。
使R成为L的根的右子树。
如下图示：
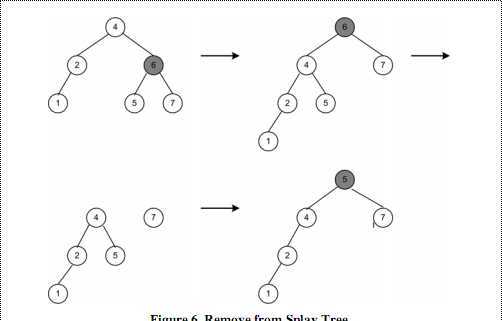
图六
六、自顶向下的伸展树：
在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，因此这种伸展树难以实现。因此，我们可以构建自顶向下的伸展树。
当我们沿着树向下搜索某个节点X的时候，我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。在伸展操作的过程中：
1、当前节点X是中树的根。
2、左树L保存小于X的节点。
3、右树R保存大于X的节点。
开始时候，X是树T的根，左右树L和R都是空的。和前面的自下而上相同，自上而下也分三种情况：
1、zig：
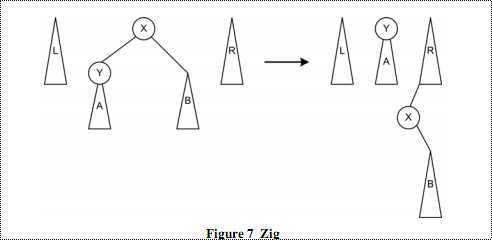
图七
如上图，在搜索到X的时候，所查找的节点比X小，将Y旋转到中树的树根。旋转之后，X及其右子树被移动到右树上。很显然，右树上的节点都大于所要查找的节点。注意X被放置在右树的最小的位置，也就是X及其子树比原先的右树中所有的节点都要小。这是由于越是在路径前面被移动到右树的节点，其值越大。读者可以分析一下树的结构，原因很简单。
2、zig-zig:
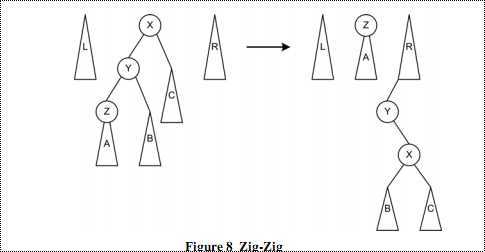
图八
在这种情况下，所查找的节点在Z的子树中，也就是，所查找的节点比X和Y都小。所以要将X，Y及其右子树都移动到右树中。首先是Y绕X右旋，然后Z绕Y右旋，最后将Z的右子树（此时Z的右子节点为Y）移动到右树中。注意右树中挂载点的位置。
3、zig-zag:
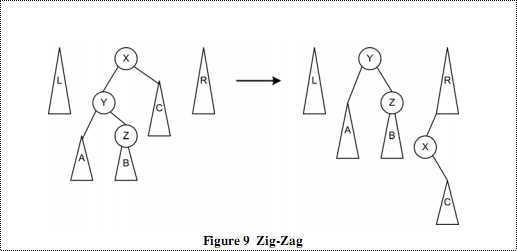图九 在这种情况中，首先将Y右旋到根。这和Zig的情况是一样的。然后变成上图右边所示的形状。接着，对Z进行左旋，将Y及其左子树移动到左树上。这样，这种情况就被分成了两个Zig情况。这样，在编程的时候就会简化，但是操作的数目增加（相当于两次Zig情况）。 最后，在查找到节点后，将三棵树合并。如图：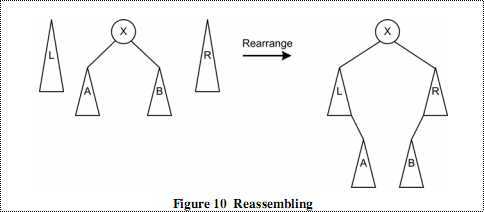 
图十
将中树的左右子树分别连接到左树的右子树和右树的左子树上。将左右树作为X的左右子树。重新最成了一所查找的节点为根的树。 下面给出伪代码：
右连接：将当前根及其右子树连接到右树上。左子结点作为新根。
左连接：将当前根及其左子树连接到左树上。右子结点作为新根。
T ： 当前的根节点。
Function Top-Down-Splay
Do
If X 小于 T Then
If X 等于 T 的左子结点 Then
右连接
ElseIf X 小于 T 的左子结点 Then
T的左子节点绕T右旋
右连接
Else X大于 T 的左子结点 Then
右连接
左连接
EndIf
ElseIf X大于 T Then
IF X 等于 T 的右子结点 Then
左连接
ElseIf X 大于 T 的右子结点 Then
T的右子节点绕T左旋
左连接
Else X小于 T 的右子结点‘ Then
左连接
右连接
EndIf
EndIf
While ！(找到 X或遇到空节点)
组合左中右树
EndFunction
同样，上面的三种情况也可以简化：
Function Top-Down-Splay
Do
If X 小于 T Then
If X 小于 T 的左孩子 Then
T的左子节点绕T右旋
EndIf
右连接
Else If X大于 T Then
If X 大于 T 的右孩子 Then
T的右子节点绕T左旋
EndIf
左连接
EndIf
While !(找到 X或遇到空节点)
组合左中右树
EndFuntion
下面是一个查找节点19的例子：
在例子中，树中并没有节点19,最后，距离节点最近的节点18被旋转到了根作为新的根。节点20也是距离节点19最近的节点，但是节点20没有成为新根，这和节点20在原来树中的位置有关系。
十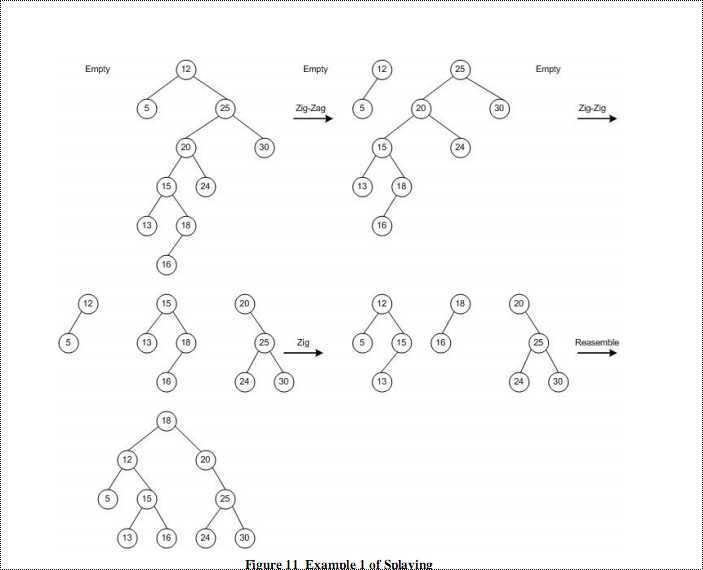 
这个例子是查找节点c：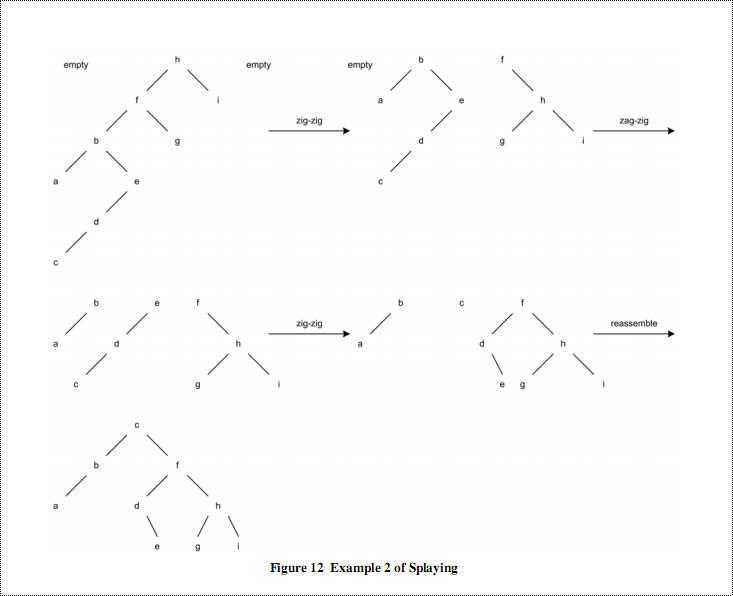 
最后，给一个用C语言实现的例子：
1 /* 2 An implementation of top-down splaying 3 D. Sleator <sleator@cs.cmu.edu> 4 March 1992 5 */ 6 #include <stdlib.h> 7 #include <stdio.h> 8 int size; /* number of nodes in the tree */ 9 /* Not actually needed for any of the operations */ 10 typedef struct tree_node Tree; 11 struct tree_node 12 { 13 Tree * left, * right; 14 int item; 15 }; 16 17 Tree * splay (int i, Tree * t) 18 { 19 /* Simple top down splay, not requiring i to be in the tree t. */ 20 /* What it does is described above. */ 21 Tree N, *l, *r, *y; 22 if (t == NULL) 23 return t; 24 N.left = N.right = NULL; 25 l = r = &N; 26 for (;;) 27 { 28 if (i < t->item) 29 { 30 if (t->left == NULL) 31 { 32 break; 33 } 34 if (i < t->left->item) 35 { 36 y = t->left; /* rotate right */ 37 t->left = y->right; 38 y->right = t; 39 t = y; 40 if (t->left == NULL) 41 { 42 break; 43 } 44 } 45 r->left = t; /* link right */ 46 r = t; 47 t = t->left; 48 } 49 else if (i > t->item) 50 { 51 if (t->right == NULL) 52 { 53 break; 54 } 55 if (i > t->right->item) 56 { 57 y = t->right; /* rotate left */ 58 t->right = y->left; 59 y->left = t; 60 t = y; 61 if (t->right == NULL) 62 { 63 break; 64 } 65 } 66 l->right = t; /* link left */ 67 l = t; 68 t = t->right; 69 } 70 else 71 { 72 break; 73 } 74 } 75 l->right = t->left; /* assemble */ 76 r->left = t->right; 77 t->left = N.right; 78 t->right = N.left; 79 return t; 80 } 81 /* Here is how sedgewick would have written this. */ 82 /* It does the same thing. */ 83 Tree * sedgewickized_splay (int i, Tree * t) 84 { 85 Tree N, *l, *r, *y; 86 if (t == NULL) 87 { 88 return t; 89 } 90 N.left = N.right = NULL; 91 l = r = &N; 92 for (;;) 93 { 94 if (i < t->item) 95 { 96 if (t->left != NULL && i < t->left->item) 97 { 98 y = t->left; 99 t->left = y->right; 100 y->right = t; 101 t = y; 102 } 103 if (t->left == NULL) 104 { 105 break; 106 } 107 r->left = t; 108 r = t; 109 t = t->left; 110 } 111 else if (i > t->item) 112 { 113 if (t->right != NULL && i > t->right->item) 114 { 115 y = t->right; 116 t->right = y->left; 117 y->left = t; 118 t = y; 119 } 120 if (t->right == NULL) 121 { 122 break; 123 } 124 l->right = t; 125 l = t; 126 t = t->right; 127 } 128 else 129 { 130 break; 131 } 132 } 133 l->right=t->left; 134 r->left=t->right; 135 t->left=N.right; 136 t->right=N.left; 137 return t; 138 } 139 140 Tree * insert(int i, Tree * t) 141 { 142 /* Insert i into the tree t, unless it‘s already there. */ 143 /* Return a pointer to the resulting tree. */ 144 Tree * new; 145 146 new = (Tree *) malloc (sizeof (Tree)); 147 if (new == NULL) 148 { 149 printf("Ran out of space\n"); 150 exit(1); 151 } 152 new->item = i; 153 if (t == NULL) 154 { 155 new->left = new->right = NULL; 156 size = 1; 157 return new; 158 } 159 t = splay(i,t); 160 if (i < t->item) 161 { 162 new->left = t->left; 163 new->right = t; 164 t->left = NULL; 165 size ++; 166 return new; 167 } 168 else if (i > t->item) 169 { 170 new->right = t->right; 171 new->left = t; 172 t->right = NULL; 173 size++; 174 return new; 175 } 176 else 177 { 178 /* We get here if it‘s already in the tree */ 179 /* Don‘t add it again */ 180 free(new); 181 return t; 182 } 183 } 184 185 Tree * delete(int i, Tree * t) 186 { 187 /* Deletes i from the tree if it‘s there. */ 188 /* Return a pointer to the resulting tree. */ 189 Tree * x; 190 if (t==NULL) 191 { 192 return NULL; 193 } 194 t = splay(i,t); 195 if (i == t->item) 196 { /* found it */ 197 if (t->left == NULL) 198 { 199 x = t->right; 200 } 201 else 202 { 203 x = splay(i, t->left); 204 x->right = t->right; 205 } 206 size--; 207 free(t); 208 return x; 209 } 210 return t; /* It wasn‘t there */ 211 } 212 213 int main(int argv, char *argc[]) 214 { 215 /* A sample use of these functions. Start with the empty tree, */ 216 /* insert some stuff into it, and then delete it */ 217 Tree * root; 218 int i; 219 root = NULL; /* the empty tree */ 220 size = 0; 221 for (i = 0; i < 1024; i++) 222 { 223 root = insert((541*i) & (1023), root); 224 } 225 printf("size = %d\n", size); 226 for (i = 0; i < 1024; i++) 227 { 228 root = delete((541*i) & (1023), root); 229 } 230 printf("size = %d\n", size); 231 } 232
标签：
原文地址：http://www.cnblogs.com/Acg-Check/p/4259231.html
