Pattern Recognition (Fourth Edition)读书笔记之mvnrnd函数

标签：

感觉是个很长的坑，大概会写很久吧。内容随机，捡遇到的拦路虎写一写。

第二章主要讲贝叶斯公式和基于贝叶斯公式的分类器。

先简单说一下mvnrnd函数的使用方法

矩阵m由t个l(l=2)维列向量构成，l维表示特征向量的维数为l，每个类有l个特征值。

t(t=3)个列向量表示群体可依据特征向量分为t类。

1 m1 = [1 1]‘;
2 m2 = [7 7]‘;
3 m3 = [15 1]‘;

三维矩阵S(l,l,t)由t个l*l方阵构成，为t个类各自的协方差矩阵covariance matrix

1 S = zeros(2,2,3);
2 S(:,:,1) =[12 0 ;0 1];
3 S(:,:,2) =[8 3 ;3 2];
4 S(:,:,3) =[2 0 ;0 2];

mvnrnd函数输出1000*l(l=2)矩阵，两列数据均值为m1,方差与协方差为S(:,:,1)

1 xans=mvnrnd(m(:,1),S(:,:,1),1000));
2 plot(xans(:,1)‘,xans(:,2)‘,‘o‘)
3 grid on

很明显，均值为1,1。行变量方差大，行分布稀疏，列变量方差小，列分布密集。

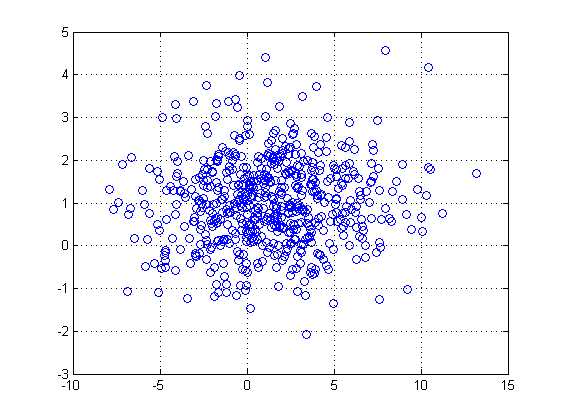
Pattern Recognition (Fourth Edition)读书笔记之mvnrnd函数

标签：

原文地址：http://www.cnblogs.com/nwpuxuezha/p/4266717.html