标签：
在写题解之前给自己打一下广告哈~
。。抱歉了，希望大家多多支持我在CSDN的视频课程，地址如下：
http://edu.csdn.net/course/detail/209
题目：
小兔的棋盘 |
| Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) |
| Total Submission(s): 802 Accepted Submission(s): 502 |
Problem Description 小兔的叔叔从外面旅游回来给她带来了一个礼物，小兔高兴地跑回自己的房间，拆开一看是一个棋盘，小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0，0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点)，这样的路径数有多少?小兔想了很长时间都没想出来，现在想请你帮助小兔解决这个问题，对于你来说应该不难吧! |
Input 每次输入一个数n(1<=n<=35)，当n等于－1时结束输入。 |
Output 对于每个输入数据输出路径数，具体格式看Sample。 |
Sample Input 1
3
12
-1 |
Sample Output 1 1 2
2 3 10
3 12 416024 |
Author Rabbit |
Source RPG专场练习赛 |
Recommend lcy |
卡特兰数的应用之一。属于“有一个n*n的矩阵，从左上角走到右上角的路径数(不能越过对角线)”。这道题其实不需要用到大数的。但是为了统一代码风格，凡是卡特兰数我都用JAVA来写。
相应的理论如下：
1）卡特兰数原本的模型可以描述如下：“对于任意数k，前k个数中-1的个数总是小于或等于1的个数”。
2）对于这道题，其实所求的路径就是“对于走到任一步k，前k步中向右的不熟总大于或等于向上的步数(否则就穿越对角线了)”>所以这道题可以使用卡特兰数来解决。
对于一个n*n的正方形网格，每次我们能向右或者向上移动一格，那么从左下角到右上角的所有在副对角线右下方的路径总数为
。同样引用Wikipedia上的一张图片来表示：
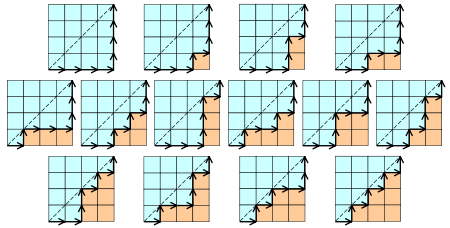
代码如下：
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static BigInteger catalans[] = new BigInteger[101];
static BigInteger four = new BigInteger("4");
static BigInteger two = new BigInteger("2");
static BigInteger one = new BigInteger("1");
/**
* 用于求卡特兰数
*/
public static void prepare(){
catalans[1] = new BigInteger("1");
int i;
for(i = 2 ; i <= 100 ; ++i){
catalans[i] = catalans[i-1].multiply(four.multiply(BigInteger.valueOf(i)).subtract(two)).divide(BigInteger.valueOf(i+1));
}
}
public static void main(String[] args) {
prepare();
Scanner scanner = new Scanner(System.in);
int t = 1;
while(scanner.hasNext()){
int n = scanner.nextInt();
if(n == -1){
return ;
}
//因为最后的结果应该是包含从左上角和右下角过去的两种解法.所以最后的结果需要乘以2
System.out.println(t++ + " " + n + " " + catalans[n].multiply(two));
}
}
}
(hdu step 2.3.8)小兔的棋盘(卡特兰数:从左上角走到右上角的路径数)
标签：
原文地址：http://blog.csdn.net/hjd_love_zzt/article/details/43484209
