标签:
茫然中不知道该做什么,更看不到希望。
偶然看到coursera上有Andrew Ng教授的机器学习课程以及他UFLDL上的深度学习课程,于是静下心来,视频一个个的看,作业一个一个的做,程序一个一个的写。N多数学的不懂、Matlab不熟悉,开始的时候学习进度慢如蜗牛,坚持了几个月,终于也学完了。为了避免遗忘,在这里记下一些内容。由于水平有限,Python也不是太熟悉,英语也不够好,有错误或不当的地方,请不吝赐教。
对于softmax背后的理论还不是很清楚,不知道是来自信息论还是概率。不过先了解个大概,先用起来,背后的理论再慢慢补充。
softmax的基本理论:
对于给定的输入x和输出有,K类分类器每类的概率为P(y=k|x,Θ),即
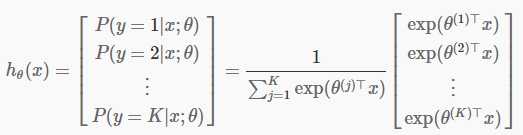
模型参数 θ(1),θ(2),…,θ(K)∈Rn ,矩阵θ以K*n的形式比较方便(其中n为输入x的维度或特征数)。
softmax回归的代价函数:
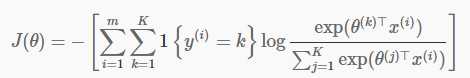
其中1{y(i)=k}为指示函数,即y(i)为k时其值为1,否则为0,或则说括号内的表达式为真时其值为1,否则为0
梯度公式:
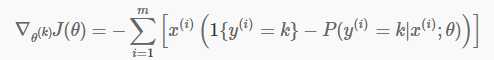
在实现此模型时遇到了2个问题,卡了一段时间:
1. 指示函数如何实现?我的实现方法:把y转换为一个k个元素的向量yv,如果y=i,则yv[i]=1,其他位置为零。在代价函数中用这个向量和概率P元素相乘、在梯度公式中与概率P相减即可实现指示函数。
2. 对矩阵不太熟练,矢量化花费了不少时间。
对概率P的参数θ进行平移得到结果和原概率一致,因此可得到参数θ是有冗余的结论。解决方法有2种,第一种是在代价函数和梯度中加上L2范式惩罚项,这种方式又增加了一个自由参数:惩罚项系数。第二种方式是固定某个类的参数为零,这样的方式不影响最终的分类结果。在我的实现方式里使用第二种方式。
教程里提到的梯度检验的方法非常有效,可以有效验证代价函数和梯度实现是否正确。只要通过梯度检验,一般都能得到正确的结果。
UFLDL教程上的练习是Matlab,由于对Matlab熟悉度不够,我使用Python+numpy+scipy来实现。
第一段代码定义了一个单一神经网络层NNLayer,它在多层神经网络中用得到。第二段代码是softmax回归的实现,它从NNLayer继承。

1 import numpy as np 2 import math 3 class NNLayer(object): 4 ‘‘‘ 5 This class is single layer of Neural network 6 ‘‘‘ 7 def __init__(self, inputSize,outputSize,Lambda,actFunc=‘sigmoid‘): 8 ‘‘‘ 9 Constructor: initialize one layer w.r.t params 10 parameters : 11 inputSize - the number of input elements 12 outputSize - the number of output 13 lambda - weight decay parameter 14 actFunc - the can be sigmoid,tanh,rectified linear function 15 ‘‘‘ 16 self.inputSize = inputSize 17 self.outputSize = outputSize 18 self.Lambda = Lambda 19 self.actFunc=sigmoid 20 self.actFuncGradient=sigmodGradient 21 22 self.activation=0 23 if actFunc==‘sigmoid‘: 24 self.actFunc = sigmoid 25 self.actFuncGradient = sigmodGradient 26 if actFunc==‘tanh‘: 27 self.actFunc = tanh 28 self.actFuncGradient =tanhGradient 29 if actFunc==‘rectfiedLinear‘: 30 self.actFunc = rectfiedLinear 31 self.actFuncGradient = rectfiedLinearGradient 32 33 #epsilon的值是一个经验公式 34 #initialize weights and intercept (bias) 35 epsilon_init = 2.4495/math.sqrt(self.inputSize+self.outputSize) 36 theta = np.random.rand(self.outputSize, self.inputSize + 1) * 2 * epsilon_init - epsilon_init 37 theta = theta*0.0001 38 ‘‘‘ 39 W=theta.reshape(self.outputSize,-1) 40 self.b=W[:,-1].reshape(self.outputSize,1) 41 self.W = W[:,:-1] 42 ‘‘‘ 43 NNLayer.rebuildTheta(self, theta) #prevent the overwriting method 44 45 def setWeight(self,Weight,b): 46 self.W = Weight 47 self.b =b 48 49 def getWeight(self): 50 return self.W,self.b 51 52 def flatTheta(self): 53 W = np.hstack((self.W, self.b)) 54 return W.ravel() 55 56 def rebuildTheta(self,theta): 57 ‘‘‘ 58 convert 1-dim theta to weight and intercept 59 Parameters: 60 theta - The vector hold the weights and intercept, needed by scipy.optimize function 61 size:outputSize*inputSize 62 ‘‘‘ 63 W=theta.reshape(self.outputSize,-1) 64 self.b=W[:,-1].reshape(self.outputSize,1) #bias b is a vector with outputSize elements 65 self.W = W[:,:-1] #weights w is a matrix with outputSize by inputSize dimension 66 67 def forward(self,X): 68 ‘‘‘ 69 Parameters: 70 X - The examples in a matrix, 71 it‘s dimensionality is inputSize by numSamples 72 ‘‘‘ 73 Z = np.dot(self.W,X)+self.b #Z 74 self.activation= self.actFunc(Z) #activations 75 return self.activation 76 77 def backpropagate(self,inputMat,delta): 78 ‘‘‘ 79 parameter: 80 inputMat - the actviations of previous layer, or input of this layer, 81 inputSize by numSamples 82 delta - the next layer error term, outputSize by numSamples 83 84 assume current layer number is l, 85 delta is the error term of layer l+1. 86 delta(l) = (W(l).T*delta(l+1)).f‘(z) 87 If this layer is the first hidden layer,this method should not 88 be called 89 The f‘ is re-writed to void the second call to the activation function 90 ‘‘‘ 91 return np.dot(self.W.T,delta)*self.actFuncGradient(inputMat) 92 93 def gradient(self,inputMat,delta): 94 ‘‘‘ 95 grad_W(l)=delta(l+1)*inputMat 96 grad_b(l) = SIGMA(delta(l+1)) 97 parameters: 98 inputMat - input of this layer, inputSize by numSamples 99 delta - the next layer error term 100 ‘‘‘ 101 m=inputMat.shape[0] 102 gw = np.dot(delta,inputMat.T)/m 103 gb = np.sum(delta,1)/m 104 #combine gradients of weights and intercepts 105 #and flat it 106 grad = np.hstack((gw, gb.reshape(-1,1))) 107 108 return np.ravel(grad) 109 110 111 def sigmoid(Z): 112 return 1.0 /(1.0 + np.exp(-Z)) 113 114 def sigmodGradient (a): 115 #a = sigmoid(Z) 116 return a*(1-a) 117 118 def tanh(Z): 119 e1=np.exp(Z) 120 e2=np.exp(-Z) 121 return (e1-e2)/(e1+e2) 122 123 def tanhGradient(a): 124 return 1-a**2 125 126 def rectfiedLinear(Z): 127 a = np.zeros(Z.shape)+Z 128 a[a<0]=0 129 return a 130 131 def rectfiedLinearGradient(a): 132 b = np.zeros(a.shape)+a 133 b[b>0]=1 134 return b
1 import numpy as np 2 import scipy.optimize as spopt 3 4 5 class SoftmaxRegression(NNLayer): 6 ‘‘‘ 7 We assume the last class weight to be zeros in this implementation. 8 The weight decay is not used here. 9 10 ‘‘‘ 11 def __init__(self, numFeatures, numClasses,Lambda=0): 12 ‘‘‘ 13 Initialization of weights,intercepts and other members 14 Parameters: 15 numClasses - The number of classes to be classified 16 X - The training samples, numFeatures by numSamples 17 y - The labels of training samples, numSamples elements vector 18 ‘‘‘ 19 20 # call the super constructor to initialize the weights and intercepts 21 # We do not need the last weights and intercepts of the last class 22 super().__init__(numFeatures, numClasses - 1, Lambda, None) 23 24 self.delta=0 25 self.numSamples=0 26 #self.X=0 27 self.inputMat=0 28 self.y_mat=0 29 30 def predict(self, Xtest): 31 ‘‘‘ 32 Prediction. 33 Before calling this method, this model should be training 34 Parameter: 35 Xtest - The data to be predicted, numFeatures by numData 36 ‘‘‘ 37 Z = np.dot(self.W, Xtest) + self.b 38 #add the prediction of the last class,they are all zeros 39 lastClass = np.zeros((1, Xtest.shape[1])) 40 Z = np.vstack((Z, lastClass)) 41 #get the index of max value in each column, it is the prediction 42 return np.argmax(Z, 0) 43 44 def forward(self): 45 ‘‘‘ 46 get the matrix of softmax hypothesis 47 this method will be called by cost and gradient methods 48 Parameters: 49 50 ‘‘‘ 51 h = np.dot(self.W, self.inputMat) + self.b 52 h = np.exp(h) 53 #add probabilities of the last class, they are all ones 54 h = np.vstack((h, np.ones((1, self.numSamples)))) 55 #The probability of all classes 56 hsum = np.sum(h, axis=0) 57 #get the probability of each class 58 self.activation = h / hsum 59 return self.activation 60 61 62 def cost(self, theta): 63 ‘‘‘ 64 The cost function. 65 Parameters: 66 theta - The vector hold the weights and intercept, needed by scipy.optimize function 67 size: (numClasses - 1)*(numFeatures + 1) 68 ‘‘‘ 69 self.rebuildTheta(theta) 70 h = np.log(self.forward()) 71 #h * self.y_mat, apply the indicator function 72 cost = -np.sum(h * self.y_mat, axis=(0, 1)) 73 74 return cost / self.numSamples 75 76 def gradient(self, theta): 77 ‘‘‘ 78 The gradient function. 79 Parameters: 80 theta - The vector hold the weights and intercept, needed by scipy.optimize function 81 size: (numClasses - 1)*(numFeatures + 1) 82 ‘‘‘ 83 self.rebuildTheta(theta) 84 h =self.forward() 85 #delta = -(self.y_mat-h) 86 self.delta = h - self.y_mat 87 self.delta=self.delta[:-1, :] 88 #get the gradient 89 grad = super().gradient(self.inputMat, self.delta) 90 91 return grad 92 93 def setTrainData(self,X,y): 94 ‘‘‘ 95 Using the training samples and labels to train the model. 96 We use function fmin_cg in scipy.optimize 97 Parameters: 98 X - The training samples, numFeatures by numSamples 99 y - The labels of training samples, numSamples elements vector 100 ‘‘‘ 101 self.setTrainingSamples(X) 102 self.setTrainingLabels(y) 103 104 def setTrainingSamples(self,X): 105 #self.X = X 106 self.inputMat=X 107 self.numSamples = X.shape[1] 108 109 def setTrainingLabels(self,y): 110 # convert Vector y to a matrix y_mat. 111 # For sample i, if it belongs to the k-th class, 112 # y_mat[k,i]=1 (k==j), y_mat[k,i]=0 (k!=j) 113 y = y.astype(np.int64) 114 yy = np.arange(self.numSamples) 115 self.y_mat = np.zeros((self.outputSize+1, self.numSamples)) 116 self.y_mat[y, yy] = 1 117 118 def train(self,X,y): 119 self.setTrainData(X,y) 120 121 theta =self.flatTheta() 122 123 #ret = spopt.fmin_l_bfgs_b(self.cost, theta, fprime=self.gradient,m=200,disp=1, maxiter=100) 124 125 #self.rebuildTheta(ret[0]) 126 opttheta = spopt.fmin_cg(self.cost, theta, fprime=self.gradient,full_output=False,disp=True, maxiter=100) 127 self.rebuildTheta(opttheta) 128 129 def performance(self,Xtest,ytest): 130 ‘‘‘ 131 Before calling this method, this model should be training 132 Parameter: 133 Xtest - The data to be predicted, numFeatures by numData 134 ‘‘‘ 135 pred = self.predict(Xtest) 136 return np.mean(pred == ytest) * 100 137 138 def checkGradient(X,y): 139 140 sm = SoftmaxRegression(X.shape[0], 10) 141 #W = np.hstack((sm.W, sm.b)) 142 sm.setTrainData(X, y) 143 theta = sm.flatTheta() 144 grad = sm.gradient(theta) 145 146 numgrad = np.zeros(grad.shape) 147 148 e = 1e-6 149 150 for i in range(np.size(grad)): 151 theta[i]=theta[i]-e 152 loss1 =sm.cost(theta) 153 theta[i]=theta[i]+2*e 154 loss2 = sm.cost(theta) 155 theta[i]=theta[i]-e 156 157 numgrad[i] = (-loss1 + loss2) / (2 * e) 158 159 print(np.sum(np.abs(grad-numgrad))/np.size(grad))
测试数据使用MNIST数据集。测试结果,正确率在92.5%左右。
测试代码:
1 X = np.load(‘../../common/trainImages.npy‘) / 255 3 y = np.load(‘../../common/trainLabels.npy‘) 4 ‘‘‘ 5 X1=X[:,:10] 6 y1=y[:10] 7 checkGradient(X1,y1) 8 ‘‘‘ 9 Xtest = np.load(‘../../common/testImages.npy‘) / 25511 ytest = np.load(‘../../common/testLabels.npy‘) 12 sm = SoftmaxRegression(X.shape[0], 10) 13 t0=time() 14 sm.train(X,y) 15 print(‘training Time %.5f s‘ %(time()-t0)) 16 17 print(‘test acc :%.3f%%‘ % (sm.performance(Xtest,ytest)))
参考资料:
Deep Learning 学习笔记(一)——softmax Regression
标签:
原文地址:http://www.cnblogs.com/arsenicer/p/4272522.html