标签:
今天把蒙皮模拟算法实现了。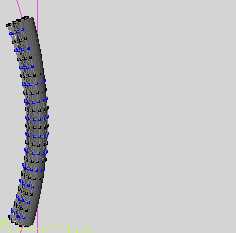

| 梯度 | Hessian | 参数增量 | ||
| 有方向参数 | G=[21319.284966 ;0.000000 ;]; | H=[ 1734695.368102 7.202621 ; 7.202621 0.000000 ; ]; | x=1.0e+03 * [0 2.9599] | |
| 没有方向参数 | G=[21319.284966 ;0.000000 ;]; | H=[ 1734695.368102 0.000000 ; 0.000000 0.000000 ; ]; | x=[0.0123 0] |
for (int ithIter = 0; ithIter < 5; ++ithIter){double f;isSucceed &= m_fem->computeValueAndGrad(p, tVec, &f, &G);p -= G * 1e-6;if(G.norm() < m_minGradSize)break;}
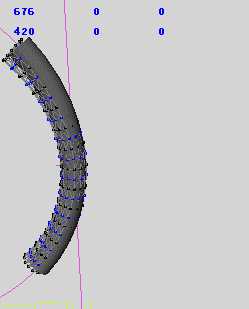
标签:
原文地址:http://www.cnblogs.com/dydx/p/4272999.html