标签:
BRDF表示的是双向反射分布函数(Bidirectional Reflectance Distribution Function),它描述了光线如何在物体表面进行反射,可以用来描述材质属性。
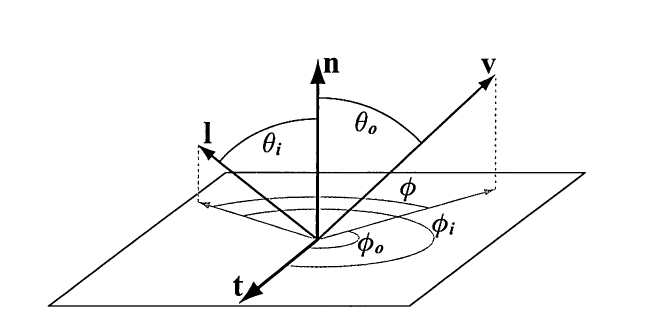
BRDF的输入参数是入射光的的仰角、方位角、出射光的仰角、方位角,还与入射光的波长相关。
BRDF的输出结果是一个数值,表示在给定的入射条件下,出射方向上反射的相对能量,另外一种理解方式是用光子的概念来考虑,BRDF给出了入射光子以特定方向离开的概率。
BRDF有一些重要的属性:
1.Helmholtz互异性(Helmholtz Reciprocity):入射角和出射角互换,函数值保持不变。
2.能量守恒:出射能量不可能大于入射能量,所以BRDF必须进行归一化处理。
BRDF在描述光线与物体相互作用方面是一个很好的抽象,但只是更一般方程的一种近似。
更一般的方程:双向表面散反射分布函数(Bidirectional Surface Scattering Reflectance Distribution)BSSRDF.
一般的BSSRDF,虽然复杂,仍然忽略了一些非常重要的变量,比如光的偏振。
BRDF没有描述内部光线散射现象。
此外,要注意,反射函数,都没有处理穿过物体表面的光线传播,只是对反射情况进行了处理。
SVBRDF: spatially varying BRDF
SBRDF: spatial BRDF
处理透射问题:BTDF
T:Trasmittance
为了处理光线传播问题,对物体表面定义了两个BRDF和两个BTDF,每侧各有一个,这样就组成了BSDF
S : Scattering
但是太过复杂的公式很少用到,通常BRDF和SVBRDF就可以描述一般物体表面。
给定一个BRDF和入射光的辐射率分布,反射方程就可以确定在给定观察方向上的出射辐射率大小,可以通过对所有方向上的入射光辐射率在物体表面以上的半球内进行积分得到。
有一种理解BRDF的方法就是在输入方向保持恒定的情况下对它进行可视化表示,用图形表示出各个方向的出射光的能量分布:
下面是几种BRDF的图形表示:

一个想法是使用微小面元对物体表面进行建模,每一个小平面都是表面上的一个小平面镜,具有随机的大小和角度。
在这些模型中,通常赋予小平面一个高斯分布的尺寸和角度(高斯分布比较简单)。
另外一种平面表示技术称为“高度相关Height Correlation”,因为小平面具有和光波长近似的尺寸,所以会出现干涉、衍射。
在物理方面需要考虑的一个重要因素是Fresnel反射,一个完整的Fresnel公式依赖于折射系数、消光系数以及入射角等因素。
计算机图形学常常会忽略偏振,可以使用两个偏振的平均值。
一些BRDF理论模型的局限性在于没有考虑各向异性的情形。
如果视点和光源位置不动,当材质的采样点绕法线方向旋转时,如果它的颜色发生变化,那么这个材质就是各向异性的。
像刷洗过的金属、上过漆的木头、织布、毛皮以及头发这样的材质都有一个确定的方向分量。
理论模型在给定材质样品的表示方面不一定有用。
另外的一种方法就是从实际物体的表面来获取BRDF数据。
测角仪、图像双向反射计,以及基于图像的方法都可以根据入射角和出射角测量得到反射信息。
有些数据库在网上是公开的。
另外一种表示BRDF的方法是用基相加(Basis Summation)技术,这些方法主要着眼于BRDF自身的形状表示。
基相加技术就是努力将BRDF的表面表示成一组函数的加权和。
《实时计算机图形学》,第二版
(转)图形学理论知识 BRDF 双向反射分布函数(Bidirectional Reflectance Distribution Function)
标签:
原文地址:http://www.cnblogs.com/aminxu/p/4274820.html