BZOJ 2301 Problem b

标签：

Description

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

2

2 5 1 5 1

1 5 1 5 2

Sample Output

14

3

HINT

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

Source

莫比乌斯反演。

反之也对。

对于此题，我们令

。

F(d)是gcd(i,j)是d的倍数的数有几个则有技术分享

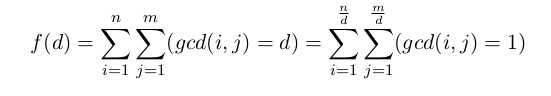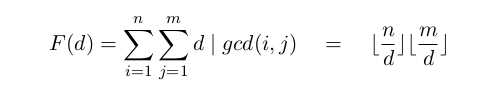，原因是i，j都有一个d的因子，所以和肯定是技术分享

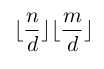，因此就可以根据反演来做了。

根据容斥原理，ans= f(a-1,c-1,k)+f(b,d,k)-f(a-1,d,k)-f(b,c-1,k)。

但是暴力枚举n再最坏情况下多组数据是肯定会tle的，但是考虑的技术分享

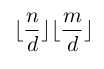变化最多√n个。对于相同的一段技术分享

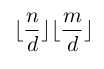，我们可以记录μ的前缀和进行计算降低复杂度。至于为什么是n/(n/i)，这个我去咨询了lyp与yxj，都没有答复，只是叫我背结论，那我就背吧。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstdlib>
 4 using namespace std;
 5 
 6 #define maxn 100010
 7 int mu[maxn],prime[maxn],tot; bool exist[maxn];
 8 
 9 inline void ready()
10 {
11     mu[1] = 1;
12     for (int i = 2;i <= 50000;++i)
13     {
14         if (!exist[i]) prime[++tot] = i,mu[i] = -1;
15         for (int j = 1;j <= tot&&i*prime[j] <= 50000;++j)
16         {
17             exist[i*prime[j]] = true;
18             if (i % prime[j] == 0) { mu[i*prime[j]] = 0; break; }
19             mu[i*prime[j]] = -mu[i];
20         }
21     }
22     for (int i = 1;i <= 50000;++i) mu[i] += mu[i-1];
23 }
24 
25 inline int work(int a,int b,int k)
26 {
27     a /= k; b /= k;
28     if (a > b) swap(a,b);
29     int ret = 0,pos;
30     for (int i = 1;i <= a;i = pos+1)
31     {
32         pos = min(a/(a/i),b/(b/i));
33         ret += (mu[pos]-mu[i-1])*(a/i)*(b/i);
34     }
35     return ret;
36 }
37 
38 int main()
39 {
40     freopen("2301.in","r",stdin);
41     freopen("2301.out","w",stdout);
42     ready();
43     int T; scanf("%d",&T);
44     while (T--)
45     {
46         int a,b,c,d,k,ans;
47         scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
48         ans = work(a-1,c-1,k)+work(b,d,k)-work(a-1,d,k)-work(b,c-1,k);
49         printf("%d\n",ans);
50     }
51     fclose(stdin); fclose(stdout);
52     return 0;
53 }

View Code

BZOJ 2301 Problem b

标签：

原文地址：http://www.cnblogs.com/mmlz/p/4275792.html