标签:
题目链接(POJ):http://poj.org/problem?id=4001
题目链接(HDOJ):http://acm.hdu.edu.cn/showproblem.php?pid=4121
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 1108 | Accepted: 299 |
Description
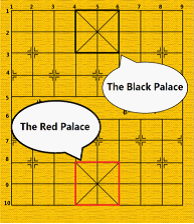
 General: the generals can move and capture one point either vertically or horizontally and cannot leave the “palace” unless the situation called “flying general” (see the right figure). “Flying general”
means that one general can “fly” across the board to capture the enemy general if they stand on the same line without intervening pieces.
General: the generals can move and capture one point either vertically or horizontally and cannot leave the “palace” unless the situation called “flying general” (see the right figure). “Flying general”
means that one general can “fly” across the board to capture the enemy general if they stand on the same line without intervening pieces. Chariot: the chariots can move and capture vertically and horizontally by any distance, but may not jump over intervening pieces
Chariot: the chariots can move and capture vertically and horizontally by any distance, but may not jump over intervening pieces Cannon: the cannons move like the chariots, horizontally and vertically, but capture by jumping exactly one piece (whether it is friendly or enemy) over to its target.
Cannon: the cannons move like the chariots, horizontally and vertically, but capture by jumping exactly one piece (whether it is friendly or enemy) over to its target. Horse: the horses have 8 kinds of jumps to move and capture shown in the left figure. However, if there is any pieces lying on a point away from the horse horizontally or vertically it cannot move or capture
in that direction (see the left figure), which is called “hobbling the horse’s leg”.
Horse: the horses have 8 kinds of jumps to move and capture shown in the left figure. However, if there is any pieces lying on a point away from the horse horizontally or vertically it cannot move or capture
in that direction (see the left figure), which is called “hobbling the horse’s leg”.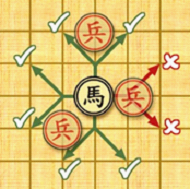
Input
Output
Sample Input
2 1 4 G 10 5 R 6 4 3 1 5 H 4 5 G 10 5 C 7 5 0 0 0
Sample Output
YES
NOHint
In the first situation, the black general is checked by chariot and “flying general”. In the second situation, the black general can move to (1, 4) or (1, 6) to stop check. See the figure above.Situation 1 Situation 2 Source
题意:给出红子和黑子的位置,判断黑子是否被将死。
题解:模拟题,根据各个棋子的行走规则,标记"杀点"即可。最后判断黑子将的活动范围是否全都在"杀点"范围内。
PS: 还是好几个月前做的这道题,一直WA。今天来处理下这个遗留问题,还很顺利,一次AC。这种题主要是思路清晰and细心
AC代码:
#include<iostream>
#include<cstring>
#define N 11
using namespace std;
int n,gx,gy,x,y,maze[N][N],pie[N][2];
char ch,chess[N][N];
int hdir[8][2]={
{-2,-1},{-2,1},{-1,2},{1,2},
{2,-1},{2,1},{-1,-2},{1,-2}
};
int Isdir[4][2]={
{-1,0},{0,1},{1,0},{0,-1}
};
bool In(int dx,int dy){
if(dx>0&&dx<11&&dy>0&&dy<11)return true;
return false;
}
void SetFlag(int dx,int dy){
int tx,ty;
switch(chess[dx][dy]){
case 'G':
tx=dx-1;
while(tx>0&&chess[tx][dy]==0){
maze[tx][dy]=0;tx--;
}
if(tx>0)maze[tx][dy]=0;
break;
case 'H':
for(int i=0;i<8;i++){
tx=dx+hdir[i][0],ty=dy+hdir[i][1];
if(In(tx,ty)&&!chess[Isdir[i/2][0]+dx][Isdir[i/2][1]+dy]){
maze[tx][ty]=0;
}
}
break;
case 'C':
for(int i=0;i<4;i++){
tx=Isdir[i][0]+dx,ty=Isdir[i][1]+dy;
while(In(tx,ty)&&!chess[tx][ty]){
tx+=Isdir[i][0];ty+=Isdir[i][1];
}
tx+=Isdir[i][0];ty+=Isdir[i][1];
while(In(tx,ty)&&!chess[tx][ty]){
maze[tx][ty]=0;
tx+=Isdir[i][0];ty+=Isdir[i][1];
}
}
break;
case 'R':
for(int i=0;i<4;i++){
int tx=Isdir[i][0]+dx,ty=Isdir[i][1]+dy;
while(In(tx,ty)&&!chess[tx][ty]){
maze[tx][ty]=0;
tx+=Isdir[i][0];ty+=Isdir[i][1];
}
if(In(tx,ty))maze[tx][ty]=0;
}
break;
}
}
int main()
{
cin.sync_with_stdio(false);
while(cin>>n>>gx>>gy&&(n||gx||gy)){
int pos=0;
memset(maze,-1,sizeof(maze));
memset(chess,0,sizeof(chess));
while(n--){
cin>>ch>>x>>y;
pie[pos][0]=x;pie[pos++][1]=y;
chess[x][y]=ch;
}
for(int i=0;i<pos;i++)
SetFlag(pie[i][0],pie[i][1]);
bool live=false;
if(maze[gx][gy])live=true;
for(int i=0;i<4;i++){
int tx=gx+Isdir[i][0],ty=gy+Isdir[i][1];
if(tx>0&&tx<4&&ty>3&&ty<7&&maze[tx][ty])live=true;
}
if(live)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
POJ Xiangqi 4001 && HDOJ 4121 Xiangqi
标签:
原文地址:http://blog.csdn.net/mummyding/article/details/43576895