标签:poj
| Time Limit: 1000MS | Memory Limit: 131072K | |||
| Total Submissions: 3494 | Accepted: 1285 | Special Judge | ||
Description
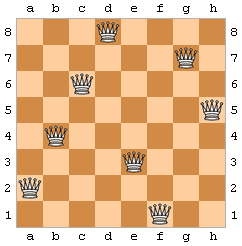
The eight queens puzzle is the problem of putting eight chess queens on an 8 × 8 chessboard such that none of them is able to capture any other. The puzzle has been generalized to arbitrary n × n boards. Given n, you are to find a solution to the n queens puzzle.
Input
The input contains multiple test cases. Each test case consists of a single integer n between 8 and 300 (inclusive). A zero indicates the end of input.
Output
For each test case, output your solution on one line. The solution is a permutation of {1, 2, …, n}. The number in the ith place means the ith-column queen in placed in the row with that number.
Sample Input
8 0
Sample Output
5 3 1 6 8 2 4 7
解题思路:
一、当n mod 6 != 2 或 n mod 6 != 3时:
[2,4,6,8,...,n],[1,3,5,7,...,n-1] (n为偶数)
[2,4,6,8,...,n-1],[1,3,5,7,...,n ] (n为奇数)
二、当n mod 6 == 2 或 n mod 6 == 3时
(当n为偶数,k=n/2;当n为奇数,k=(n-1)/2)
[k,k+2,k+4,...,n],[2,4,...,k-2],[k+3,k+5,...,n-1],[1,3,5,...,k+1] (k为偶数,n为偶数)
[k,k+2,k+4,...,n-1],[2,4,...,k-2],[k+3,k+5,...,n-2],[1,3,5,...,k+1],[n] (k为偶数,n为奇数)
[k,k+2,k+4,...,n-1],[1,3,5,...,k-2],[k+3,...,n],[2,4,...,k+1] (k为奇数,n为偶数)
[k,k+2,k+4,...,n-2],[1,3,5,...,k-2],[k+3,...,n-1],[2,4,...,k+1],[n ] (k为奇数,n为奇数)
(上面有六条序列。一行一个序列,中括号是我额外加上的,方便大家辨认子序列,子序列与子序列之间是连续关系,无视中括号就可以了。第i个数为ai,表示在第i行ai列放一个皇后;... 省略的序列中,相邻两数以2递增。)
参考代码:#include<iostream>
#include<cmath>
using namespace std;
int main(int i)
{
int n; //皇后数
while(cin>>n)
{
if(!n)
break;
if(n%6!=2 && n%6!=3)
{
if(n%2==0) //n为偶数
{
for(i=2;i<=n;i+=2)
cout<<i<<' ';
for(i=1;i<=n-1;i+=2)
cout<<i<<' ';
cout<<endl;
}
else //n为奇数
{
for(i=2;i<=n-1;i+=2)
cout<<i<<' ';
for(i=1;i<=n;i+=2)
cout<<i<<' ';
cout<<endl;
}
}
else if(n%6==2 || n%6==3)
{
if(n%2==0) //n为偶数
{
int k=n/2;
if(k%2==0) //k为偶数
{
for(i=k;i<=n;i+=2)
cout<<i<<' ';
for(i=2;i<=k-2;i+=2)
cout<<i<<' ';
for(i=k+3;i<=n-1;i+=2)
cout<<i<<' ';
for(i=1;i<=k+1;i+=2)
cout<<i<<' ';
cout<<endl;
}
else //k为奇数
{
for(i=k;i<=n-1;i+=2)
cout<<i<<' ';
for(i=1;i<=k-2;i+=2)
cout<<i<<' ';
for(i=k+3;i<=n;i+=2)
cout<<i<<' ';
for(i=2;i<=k+1;i+=2)
cout<<i<<' ';
cout<<endl;
}
}
else //n为奇数
{
int k=(n-1)/2;
if(k%2==0) //k为偶数
{
for(i=k;i<=n-1;i+=2)
cout<<i<<' ';
for(i=2;i<=k-2;i+=2)
cout<<i<<' ';
for(i=k+3;i<=n-2;i+=2)
cout<<i<<' ';
for(i=1;i<=k+1;i+=2)
cout<<i<<' ';
cout<<n<<endl;
}
else //k为奇数
{
for(i=k;i<=n-2;i+=2)
cout<<i<<' ';
for(i=1;i<=k-2;i+=2)
cout<<i<<' ';
for(i=k+3;i<=n-1;i+=2)
cout<<i<<' ';
for(i=2;i<=k+1;i+=2)
cout<<i<<' ';
cout<<n<<endl;
}
}
}
}
return 0;
}
poj3239 Solution to the n Queens Puzzle (n皇后问题)
标签:poj
原文地址:http://blog.csdn.net/codeforcer/article/details/43575193