标签:
平滑曲线生成是一个很实用的技术
很多时候,我们都需要通过绘制一些折线,然后让计算机平滑的连接起来,或者是生成一些平滑的面
这里介绍利用一种贝塞尔曲线拟合的方法,先给出我们最终的效果
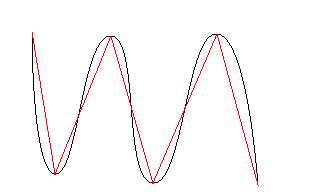
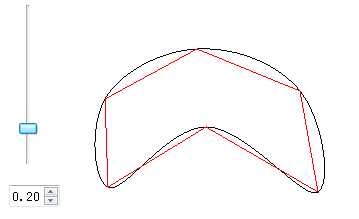
图1 、折线拟合 图2、多边形拟合(封闭的折线)
继续阅读本文之前,你需要先掌握贝塞尔曲线的基本知识,这个网上资料很多,这里直接给出源代码

//count为插入点数, outPoints为输出点集合,长度为count + 2(含首尾) void BezierHelper::parseBezier(const Ogre::Vector2& start, const Ogre::Vector2& end, const Ogre::Vector2& control1, const Ogre::Vector2& control2, int count, std::vector<Ogre::Vector2>& outPoints) { if(count < 0) count = Bezier3DefaultPointNum; outPoints.push_back(start); for(int i = 1; i<=count; i++) { double st = (double) i/(count+1); double dt = (1-st); //二次项 double st2 = st * st; double dt2 = dt * dt; double t0 = dt * dt2; double t1 = dt2 * st * 3; double t2 = dt * st2 * 3; double t3 = st * st2; outPoints.push_back(start * t0 + control1 * t1 + control2 * t2 + end * t3); } outPoints.push_back(end); }
注:本文实现使用了Ogre的Vector2类,是一个表示二维坐标点的结构,
因为其同时重载了常用了+-*/等算数运算,代码看起来会比较简洁,本文最后会附上裁剪的Vector2源文件
算法原理:
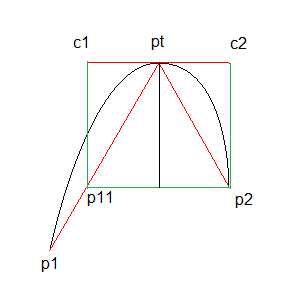
图3:当前点pt,当前点前后两点p1、p2, pt点对应的前后控制点c1、c2
参考图3,对于p1-pt-p2两段线,算法生成p1~pt 和 pt~p2两条贝塞尔曲线
两条贝塞尔曲线在pt点对应的控制点分别为c1、c2
因为贝塞尔曲线与该点和其控制点的连线相切,所以保证c1、pt、c2三点共线就可以产生平滑的曲线
手工控制各控制点是很繁琐的,如何自动计算控制点是本算法的核心,算法实现方式为:
实现:
1 //根据当前点pt,前一点p1, 后一点p2计算当前点对应的控制点control1 control2 2 void BezierHelper::getControlPoint(const Ogre::Vector2& pt, const Ogre::Vector2& p1, const Ogre::Vector2& p2, 3 Ogre::Vector2& control1, Ogre::Vector2& control2, double ratio) 4 { 5 double length1 = (p1 - pt).length(); 6 double length2 = (p2 - pt).length(); 7 8 double v = length2/(length1+ 0.000001); 9 10 Ogre::Vector2 delta; 11 if(v>1) 12 { 13 delta = p1 - (pt + ( p2 - pt) / (v + 0.000001)); 14 } 15 else 16 { 17 delta = pt + (p1-pt) * v - p2 ; 18 } 19 20 delta *= ratio; 21 control1 = pt + delta; 22 control2 = pt - delta; 23 }
ratio参数为调整系数,因为相对与总长,一般取0.1-0.3之间
同样方法可以计算p1,p2的前后控制点,这样通过p1和p1的后控制点、pt和c1可以绘制曲线p1~pt,依次类推....
对于首尾节点,可以简单的取其控制点为自身
实现:
void BezierHelper::parsePolyline(const std::vector<Ogre::Vector2>& points, int count, std::vector<Ogre::Vector2>& outPoints, double ratio) { std::vector<Ogre::Vector2>::size_type pointsSize = points.size(); if(pointsSize < 3 )//插值至少需要三点 { for(int i = 0; i<pointsSize; i++) { outPoints.push_back(points[i]); } } else { Ogre::Vector2 control1, control2; //顶点对应的前后控制点 getControlPoint(points[1], points[0], points[2], control1, control2, ratio); //首端 _parseBezier(points[0], points[1], points[0], control1, count, outPoints); for(int i = 2; i<pointsSize -1; i++) //根据中间各点生成与前一点连线 { Ogre::Vector2 lastControl = control2; getControlPoint(points[i], points[i-1], points[i+1], control1, control2, ratio); _parseBezier(points[i - 1], points[i], lastControl, control1, count, outPoints); } _parseBezier(points[pointsSize-2], points[pointsSize-1], control2, points[pointsSize-1], count, outPoints); outPoints.push_back(points[pointsSize-1]); } }
在运行这段代码之前,我们需要修改前面的parseBezier函数为_parseBezier,区别仅在于不包括尾节点,方便折线、多边形生成代码的调用:

void BezierHelper::_parseBezier(const Ogre::Vector2& start, const Ogre::Vector2& end, const Ogre::Vector2& control1, const Ogre::Vector2& control2, int count, std::vector<Ogre::Vector2>& outPoints) { if(count < 0) count = Bezier3DefaultPointNum; outPoints.push_back(start); for(int i = 1; i<=count; i++) { double st = (double) i/(count+1); double dt = (1-st); //二次项 double st2 = st * st; double dt2 = dt * dt; double t0 = dt * dt2; double t1 = dt2 * st * 3; double t2 = dt * st2 * 3; double t3 = st * st2; outPoints.push_back(start * t0 + control1 * t1 + control2 * t2 + end * t3); } }
与折线区别仅在于首点控制点需要通过尾节点生成,尾节点需要利过首节点生成
实现:

void BezierHelper::parsePolygon(const std::vector<Ogre::Vector2>& points, int count, std::vector<Ogre::Vector2>& outPoints, double ratio) { std::vector<Ogre::Vector2>::size_type pointsSize = points.size(); if(pointsSize < 3 )//插值至少需要三点 { for(int i = 0; i<pointsSize; i++) { outPoints.push_back(points[i]); } } else { Ogre::Vector2 control1, control2; //顶点对应的前后控制点 Ogre::Vector2 firstControl; Ogre::Vector2 lastControl; //首尾 getControlPoint(points[pointsSize-1], points[pointsSize-2], points[0], firstControl, lastControl, ratio); getControlPoint(points[0], points[pointsSize-1], points[1], control1, control2, ratio); _parseBezier(points[pointsSize-1], points[0], lastControl, control1, count, outPoints); for(int i = 1; i<pointsSize-1; i++) //根据中间各点,生成与前一点连线 { lastControl = control2; getControlPoint(points[i], points[i-1], points[i+1], control1, control2, ratio); _parseBezier(points[i-1], points[i], lastControl, control1, count, outPoints); } parseBezier(points[pointsSize-2], points[pointsSize-1], control2, firstControl, count, outPoints); //末端 outPoints.pop_back(); } }
附:Ogre::Vector2

#ifndef __Vector2_H__ #define __Vector2_H__ #include <assert.h> namespace Ogre { class Vector2 { public: double x, y; public: inline Vector2() { } inline Vector2(const double fX, const double fY ) : x( fX ), y( fY ) { } inline Vector2& operator = ( const Vector2& rkVector ) { x = rkVector.x; y = rkVector.y; return *this; } inline Vector2& operator = ( const double fScalar) { x = fScalar; y = fScalar; return *this; } inline bool operator == ( const Vector2& rkVector ) const { return ( x == rkVector.x && y == rkVector.y ); } inline bool operator != ( const Vector2& rkVector ) const { return ( x != rkVector.x || y != rkVector.y ); } // arithmetic operations inline Vector2 operator + ( const Vector2& rkVector ) const { return Vector2( x + rkVector.x, y + rkVector.y); } inline Vector2 operator - ( const Vector2& rkVector ) const { return Vector2( x - rkVector.x, y - rkVector.y); } inline Vector2 operator * ( const double fScalar ) const { return Vector2( x * fScalar, y * fScalar); } inline Vector2 operator * ( const Vector2& rhs) const { return Vector2( x * rhs.x, y * rhs.y); } inline Vector2 operator / ( const double fScalar ) const { assert( fScalar != 0.0 ); double fInv = 1.0f / fScalar; return Vector2( x * fInv, y * fInv); } inline Vector2 operator / ( const Vector2& rhs) const { return Vector2( x / rhs.x, y / rhs.y); } inline const Vector2& operator + () const { return *this; } inline Vector2 operator - () const { return Vector2(-x, -y); } // overloaded operators to help Vector2 inline friend Vector2 operator * ( const double fScalar, const Vector2& rkVector ) { return Vector2( fScalar * rkVector.x, fScalar * rkVector.y); } inline friend Vector2 operator / ( const double fScalar, const Vector2& rkVector ) { return Vector2( fScalar / rkVector.x, fScalar / rkVector.y); } inline friend Vector2 operator + (const Vector2& lhs, const double rhs) { return Vector2( lhs.x + rhs, lhs.y + rhs); } inline friend Vector2 operator + (const double lhs, const Vector2& rhs) { return Vector2( lhs + rhs.x, lhs + rhs.y); } inline friend Vector2 operator - (const Vector2& lhs, const double rhs) { return Vector2( lhs.x - rhs, lhs.y - rhs); } inline friend Vector2 operator - (const double lhs, const Vector2& rhs) { return Vector2( lhs - rhs.x, lhs - rhs.y); } // arithmetic updates inline Vector2& operator += ( const Vector2& rkVector ) { x += rkVector.x; y += rkVector.y; return *this; } inline Vector2& operator += ( const double fScaler ) { x += fScaler; y += fScaler; return *this; } inline Vector2& operator -= ( const Vector2& rkVector ) { x -= rkVector.x; y -= rkVector.y; return *this; } inline Vector2& operator -= ( const double fScaler ) { x -= fScaler; y -= fScaler; return *this; } inline Vector2& operator *= ( const double fScalar ) { x *= fScalar; y *= fScalar; return *this; } inline Vector2& operator *= ( const Vector2& rkVector ) { x *= rkVector.x; y *= rkVector.y; return *this; } inline Vector2& operator /= ( const double fScalar ) { assert( fScalar != 0.0 ); double fInv = 1.0f / fScalar; x *= fInv; y *= fInv; return *this; } inline Vector2& operator /= ( const Vector2& rkVector ) { x /= rkVector.x; y /= rkVector.y; return *this; } /** Returns the length (magnitude) of the vector. @warning This operation requires a square root and is expensive in terms of CPU operations. If you don‘t need to know the exact length (e.g. for just comparing lengths) use squaredLength() instead. */ inline double length () const { return sqrt( x * x + y * y ); } /** Returns the square of the length(magnitude) of the vector. @remarks This method is for efficiency - calculating the actual length of a vector requires a square root, which is expensive in terms of the operations required. This method returns the square of the length of the vector, i.e. the same as the length but before the square root is taken. Use this if you want to find the longest / shortest vector without incurring the square root. */ inline double squaredLength () const { return x * x + y * y; } /** Returns the distance to another vector. @warning This operation requires a square root and is expensive in terms of CPU operations. If you don‘t need to know the exact distance (e.g. for just comparing distances) use squaredDistance() instead. */ inline double distance(const Vector2& rhs) const { return (*this - rhs).length(); } /** Returns the square of the distance to another vector. @remarks This method is for efficiency - calculating the actual distance to another vector requires a square root, which is expensive in terms of the operations required. This method returns the square of the distance to another vector, i.e. the same as the distance but before the square root is taken. Use this if you want to find the longest / shortest distance without incurring the square root. */ inline double squaredDistance(const Vector2& rhs) const { return (*this - rhs).squaredLength(); } /** Calculates the dot (scalar) product of this vector with another. @remarks The dot product can be used to calculate the angle between 2 vectors. If both are unit vectors, the dot product is the cosine of the angle; otherwise the dot product must be divided by the product of the lengths of both vectors to get the cosine of the angle. This result can further be used to calculate the distance of a point from a plane. @param vec Vector with which to calculate the dot product (together with this one). @return A float representing the dot product value. */ inline double dotProduct(const Vector2& vec) const { return x * vec.x + y * vec.y; } /** Normalises the vector. @remarks This method normalises the vector such that it‘s length / magnitude is 1. The result is called a unit vector. @note This function will not crash for zero-sized vectors, but there will be no changes made to their components. @return The previous length of the vector. */ inline double normalise() { double fLength = sqrt( x * x + y * y); // Will also work for zero-sized vectors, but will change nothing // We‘re not using epsilons because we don‘t need to. // Read http://www.ogre3d.org/forums/viewtopic.php?f=4&t=61259 if ( fLength > double(0.0f) ) { double fInvLength = 1.0f / fLength; x *= fInvLength; y *= fInvLength; } return fLength; } /** Returns a vector at a point half way between this and the passed in vector. */ inline Vector2 midPoint( const Vector2& vec ) const { return Vector2( ( x + vec.x ) * 0.5f, ( y + vec.y ) * 0.5f ); } /** Returns true if the vector‘s scalar components are all greater that the ones of the vector it is compared against. */ inline bool operator < ( const Vector2& rhs ) const { if( x < rhs.x && y < rhs.y ) return true; return false; } /** Returns true if the vector‘s scalar components are all smaller that the ones of the vector it is compared against. */ inline bool operator > ( const Vector2& rhs ) const { if( x > rhs.x && y > rhs.y ) return true; return false; } /** Sets this vector‘s components to the minimum of its own and the ones of the passed in vector. @remarks ‘Minimum‘ in this case means the combination of the lowest value of x, y and z from both vectors. Lowest is taken just numerically, not magnitude, so -1 < 0. */ inline void makeFloor( const Vector2& cmp ) { if( cmp.x < x ) x = cmp.x; if( cmp.y < y ) y = cmp.y; } /** Sets this vector‘s components to the maximum of its own and the ones of the passed in vector. @remarks ‘Maximum‘ in this case means the combination of the highest value of x, y and z from both vectors. Highest is taken just numerically, not magnitude, so 1 > -3. */ inline void makeCeil( const Vector2& cmp ) { if( cmp.x > x ) x = cmp.x; if( cmp.y > y ) y = cmp.y; } /** Generates a vector perpendicular to this vector (eg an ‘up‘ vector). @remarks This method will return a vector which is perpendicular to this vector. There are an infinite number of possibilities but this method will guarantee to generate one of them. If you need more control you should use the Quaternion class. */ inline Vector2 perpendicular(void) const { return Vector2 (-y, x); } /** Calculates the 2 dimensional cross-product of 2 vectors, which results in a single floating point value which is 2 times the area of the triangle. */ inline double crossProduct( const Vector2& rkVector ) const { return x * rkVector.y - y * rkVector.x; } /** Returns true if this vector is zero length. */ inline bool isZeroLength(void) const { double sqlen = (x * x) + (y * y); return (sqlen < (1e-06 * 1e-06)); } /** As normalise, except that this vector is unaffected and the normalised vector is returned as a copy. */ inline Vector2 normalisedCopy(void) const { Vector2 ret = *this; ret.normalise(); return ret; } /** Calculates a reflection vector to the plane with the given normal . @remarks NB assumes ‘this‘ is pointing AWAY FROM the plane, invert if it is not. */ inline Vector2 reflect(const Vector2& normal) const { return Vector2( *this - ( 2 * this->dotProduct(normal) * normal ) ); } }; } #endif
标签:
原文地址:http://www.cnblogs.com/wiki3d/p/4275961.html