题目大意：从一个数字集合中取出两个最大的相加得到的结果和原来的两个数再放回集合，求经过k次操作后，集合元素和的最大值

题目分析：因为每次肯定找最大的两个相加，开始有a b假设a比b小
num      a     b         a+b         a+2b        2a+3b...
sum      a     a+b     2a+2b     3a+4b      5a+7b...
类似斐波那契数列sum[i] = sum[i - 1] + num[i - 1] + num[i - 2]
由此我们推出转移矩阵：

ans = (A^k * B) % MOD，采用矩阵快速幂

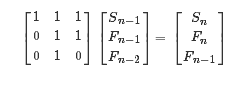
#include <cstring>
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int const MOD = 10000007;

struct matrix
{
    ll m[3][3];
};
int a[100010];

matrix multiply(matrix x, matrix y)  //矩阵乘法
{
    matrix tmp;
    memset(tmp.m, 0, sizeof(tmp.m));
    for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
        {
            if(x.m[i][j] == 0) 
                continue;
            for(int k = 0; k < 3; k++)
            {
                if(y.m[j][k] == 0) 
                    continue;
                tmp.m[i][k] += x.m[i][j] * y.m[j][k] % MOD;
                tmp.m[i][k] %= MOD;
            }
        }
    }
    return tmp;
}

matrix quickmod(matrix a, int n) //矩阵快速幂
{
    matrix res;
    memset(res.m, 0, sizeof(res.m));
    for(int i = 0; i < 3; i++) 
        res.m[i][i] = 1;
    while(n)
    {
        if(n & 1)
            res = multiply(res, a);
        n >>= 1;
        a = multiply(a, a);
    }
    return res;
}
int main()
{
    int n, k;
    while(scanf("%d %d", &n, &k) != EOF)
    {
        ll sum = 0;
        for(int i = 0; i < n; i++)
        {
            scanf("%d", &a[i]);
            sum += a[i];
        }
        sort(a, a + n);
        matrix tmp;
        tmp.m[0][0] = 1; tmp.m[0][1] = 1; tmp.m[0][2] = 1;
        tmp.m[1][0] = 0; tmp.m[1][1] = 1; tmp.m[1][2] = 1;
        tmp.m[2][0] = 0; tmp.m[2][1] = 1; tmp.m[2][2] = 0;
        tmp = quickmod(tmp, k);
        ll ans = (tmp.m[0][0] * sum + tmp.m[0][1] * a[n - 1] + tmp.m[0][2] * a[n - 2]) % MOD;
        printf("%lld\n", ans);
    }
}