标签:
一:题目大意
当给定一个数时,先求出它的所有因子N1,N2······Nk,然后求出它的因子对应的因子的个数n1,n2·····nk,并求出最终结果S=n1^3+n2^3+n3^3+·····+nk^3.
二:题目分析
本题的数据范围是N<2^31。如果对于每一趟直接判断时间复杂度将会很高。因此我们需要做预处理,先求出在最大范围内所有的质数。
对于每一个质数p,它的因子只有1和p本身,那么S(p)=1+2^3=9.
对于数字x=p^k,我们可以得知它有1,p,,,,p^k这么多因子,那么S(x)=1+2^3+······+(k+1)^3.
我们首先定义n(x)表示x的因子个数。如果N有两个不同的素因子p1和p2,这时不妨设N=p1^k1*p2^k2.这时我们可以得出一个事实:
n(p1^i*p2^j)=(j+1)n(p1^i)。
则很容易得到:
S(N)=S(p1^k1)+S(p2*p1^k1)+S(p2^2*p1^k1)+····+S(p2^k2*p1^k1)
下面我们继续往后推论:
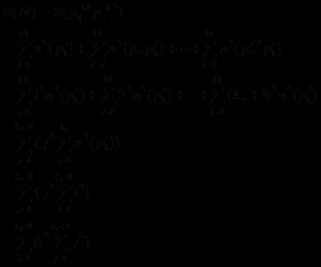
采用类似的方法我们可以得出对于任意

我们有:
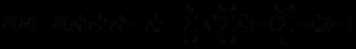
分析到这里我们可以着手写代码了。
三 :AC代码
#include<iostream> #include<vector> using namespace std; int isprime[1<<16]; const int maxi=1<<16; vector<int>p; void pre() { for(int i=2;i<maxi;i++) if(!isprime[i]) { for(int k=i+i;k<maxi;k+=i) { isprime[k]=1; } p.push_back(i); } } int cal(int N) { int ans=1; int i=0; while(p[i]*p[i]<=N&&i<p.size()) { if(N%p[i]==0) { int k=1; int j=1; while(N%p[i]==0) { k++; j+=k*k*k; N/=p[i]; } ans*=j; } i++; } if(N!=1) ans*=9; return ans; } int main() { int T; pre(); cin>>T; int n; while(T--) { cin>>n; cout<<cal(n)<<endl; } return 0; }
四:学会合理运用数字之间的关系转化问题是解题的关键。
中山大学校队内部选拔赛试题3.1【Factorial Factors】--------2015年2月9日
标签:
原文地址:http://www.cnblogs.com/khbcsu/p/4282643.html