标签:
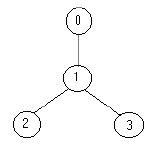
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0) 5 3:(3) 1 4 2 1:(1) 0 2:(0) 0:(0) 4:(0)
1 2
还是对树地守卫问题,不过这题是守卫所有的边。节点可以安排士兵,其能守卫相邻的边。求用最少的士兵,守卫所有的边。与皇宫守卫不同。这里只需要看节点是否安排守卫。如果不安排,则其所有子节点均要安排,如果安排守卫,则其子节点状态随意。
//dp[t][0/1] : 根节点为t的子树(0:根节点不安排守卫1:安排)的所有边被守卫的情况下的最小安排士兵数量。 dp[t][0] = sum(dp[ti][1]); dp[t][1] = sum(min(dp[ti][0], dp[ti][1]));
#include <cstdio> #include <vector> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int INF = 999999999; int n; std::vector<int > v[2005]; bool vis[2005]; int dp[2005][2]; void Tdp(int t) { if (v[t].size() == 0) { dp[t][0] = 0; dp[t][1] = 1; return ; } for (int i=0; i<v[t].size(); i++) { Tdp(v[t][i]); dp[t][0] += dp[v[t][i]][1]; dp[t][1] += min(dp[v[t][i]][0], dp[v[t][i]][1]); } dp[t][1]++; } void init() { memset(dp, 0, sizeof(dp)); memset(vis, false, sizeof(vis)); for (int i=0; i<1505; i++) { v[i].clear(); } } int main () { while (scanf ("%d",&n)!=EOF) { init(); for (int i=0; i<n; i++) { int a, b, c; scanf ("%d:(%d)", &a, &b); for (int j=0; j<b; j++) { scanf ("%d", &c); v[a].push_back(c); vis[c] = true; } } int root; for (int i=0; i<n; i++) { if (!vis[i]) { root = i; break; } } Tdp(root); cout << min(dp[root][0], dp[root][1]) << endl; } return 0; }
<!--话说这输入真他妈恶心-->
标签:
原文地址:http://www.cnblogs.com/xuelanghu/p/4284354.html