标签：
转载请注明出处：http://www.cnblogs.com/ymingjingr/p/4271742.html
训练与测试。
回顾以及预览。
首先回顾一下上一章学过的内容，学习在何种情况下是可行的。
在可学习的数据来自于一个统一的分布（distribution），且假设空间中的假设函数为有限个的情况下，其学习流程图如图5-1所示。
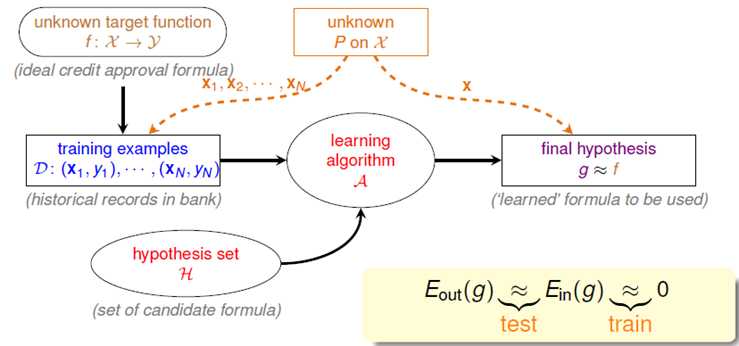
图5-1 一种可行的学习流程图
此图和前几章中的流程图最大的不同是加入了一个模块，准确的说是一种假设情况，假设训练数据样本和未知的测试样本来自同一的分布（这点尤为重要现有的大部分机器学习算法都从这点出发，好像迁移学习不是），并且假设空间的假设是有限的情况下，即|H| = M，M是有限的值，在训练样本N足够大，假设空间中的所有的假设都会遵循PAC准则，确保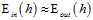
，每一个假设函数都可以满足近似相等的性质，因此可以通过算法在这些假设空间中找一个
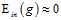的假设，同样PAC也保证了
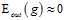。因此可以说机器学习在这种情况下是可行的。（训练样本和测试样本满足同分布，假设空间有限，并且训练数据足够大）
接着回顾一下之前四章的内容：
第一章介绍了存在一个未知的目标函数f，机器学习的任务是找出一个假设函数g，使得假设g和目标函数f很接近，即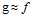
，用第四章的概念可以解释为在测试时的错误率接近零，即
。
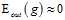第二章介绍了在训练时使假设函数g和目标函数f很接近就可以了，用第四章的概念可以解释为训练时的错误率接近零，即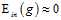
。
第三章介绍了一种机器学习最基础、最核心的方法：使用批量的数据和监督式的学习来做二元分类。
第四章介绍了在假设空间不是太多，即假设函数有限的情况下，训练时的错误率和测试时的错误率很接近，即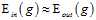
。
从以上各章节中可以看出将机器学习分为了两个主要问题来解决：
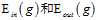是足够接近的？这是连接第一章和第二章的桥梁。
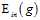足够小？这是第二章的内容，当然后面的章节还会继续介绍其他的技巧。在第四章中介绍的假设空间的大小M与上述两个问题存在何种关系？通过一个表格进行分析，如表5-1所示。
表5-1 M的大小与两个条件的关系
|
M很小的时候 |
M很大的时候 |
|
|
第一个问题
|
满足， M小的时候，两者不相等的几率变小了 |
不满足， M大的时候，两者不相等的几率变大了 |
|
第二个问题
|
不满足，在M变小时，假设的数量变小，算法的选择变小，可能无法找到 |
满足，在M变大时，假设的数量变大，算法的选择变大，找到 |
显然M趋于无穷大时，表现非常不好，如何解决这个问题呢？
需要寻找一个小于无限大M的替代值，并且这个值还和假设空间有关系，用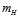
表示。以后的几章中讨论如何在M为无限大时，保证
。
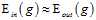线的有效数量。
第四章的结尾求出了在有限假设空间中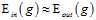
的上限，当时，使用联合上限（union bound），实际不等式的上界被放大了太多。假设在假设空间中包含无限多的假设函数，则此上限为无穷大，而真正合理的上界是不应该大于1（因为是个概率问题，其最大值也不会超过1）。
造成这一问题的原因是什么呢？很容易想到这个联合上界是不是过于宽松了。对，问题确实出在此处，学过集合的同学肯定都知道，两个集合的或集写成两个集合相加的形式时，一定要减去它俩的交集。而我们这里的问题出在，这几个集合不仅相交，而且交集很大，却没有被减掉，因此上界过于宽松。
继续回到假设空间的问题上，两个假设函数出现完全相同坏数据的可能性很大，如上一章表4-3的h2和h3就出现了几个相同的坏数据。举个简单的例子，在二维平面上进行二元线性分类，假设两条直线h1和h2很接近，那么就不难得出两种假设的坏数据也基本重叠，其实这种数据的分布应为图5-2所示。
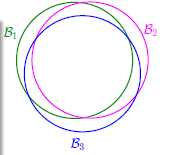
图5-2 不好数据的分布
如果可以将这无限大的假设空间分成有限的几类，按照样本数据划分方式进行分类，如是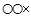
和
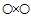被定义为两种不同的类别。这一思路的原因个人认为有两个：一是这本身就是一个数据分类错误率的问题，从数据分类方式着手也很切要害；二是训练样本必然是有限的，分类的方式也是有限的，可以将无限的问题转换成有限的问题。
先从最简单的分一个样本点着手，假设是一个二元线性分类问题，一个样本的例子比较容易理解，如图 5-3所示。
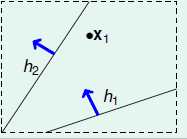
图5-3 单一训练样本分类问题
一个样本点分类可以有几种方式？无非两种，该样本为正，或者为负。而假设空间中的所有假设或者称之为直线，都只能分属于这两种情况。
继续观察两个样本的情况，如图5-4所示。
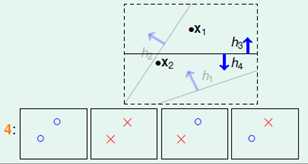
图5-4 两个训练样本分类问题
这种情况可以分为如图所示的4种情况，也就是所有的直线可以分属这4个类中。
继续观察三个样本的情况，如图5-5所示。
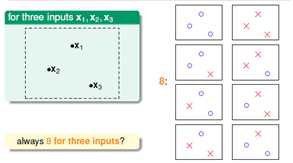
图5-5三个训练样本分类问题
出现了8种情况，但是如果样本的分布转变一下呢？比如三排成一线，就只有6类，如图5-6所示。
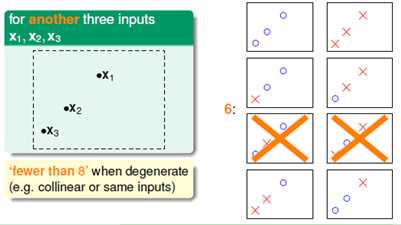
图5-6三个训练样本排成一条直线的分类问题
继续观察四个样本的情况，如图5-7所示。
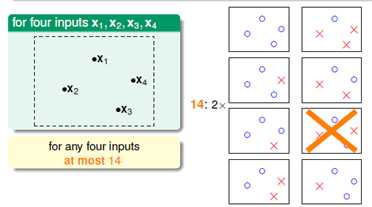
图5-7四个训练样本分类问题
说明一下此处只画了8种情况（其中一种还不可能线性可分），因为直接将其颠倒就可以得到剩下的8种情况，完全是对称的，所示总共有14种可以划分的种类。
不再无休止的继续举例，做一个总结。从上述内容可以看出，将无限多的假设和有限多的训练数据建立了一种关系，如图5-为是样本为二维时，二元线性可分的类型与样本数量的关系图。
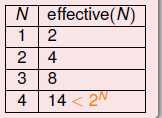
图5-7二元线性可分的类型与样本数量的关系图
从图中可以推到出下述公式成立，如公式5-1所示。
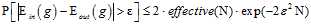（公式5-1）
其中N在大于3的情况下，必然远小于2的N次方。其实即使是等于2的N次方，也可以说明右边的式子在N趋于无穷大的情况下是一个趋近于零的值，原因很简单，e这个自然常数的值大于2.7也大于2，因此右式是个递减函数，此处不做过多的推导了。
超平面的有效数量。
上一节的内容介绍了，将无限多的假设转换成为有限多种类型上。
这种以训练样本的分类情况来确定一类假设的方式，称之为二分类（dichotomy），使用符号表示为H(x1,x2,…,xN)，即假设空间在特定的训练样本集合（x1,x2,…,xN）上被分为几类。如表5-2所示，对二分类空间与假设空间做出比较。
表5-2 假设空间与二分空间的对比
|
假设空间H |
二分H(x1,x2,…,xN) |
|
|
举例 |
在空间中所有的线 |
{○○×, ○○○, ○××,..} |
|
大小 |
无限大 |
上限为 |
以二元线性可分的情况举例，假设空间是在二维平面上的所有直线，它一定是无限的；而二分空间就是能将二维平面上的样本点划分为不同情况的直线种类（不同情况具体是什么意思，参见上一节），而它最多只是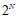
，因此是有限的。
现在的思路就是使用H(x1,x2,…,xN)的大小来取代无限大的M，如何取代呢？
会发现H(x1,x2,…,xN)的取值取决于训练样本的分布情况，因此要取消这种依赖的关系，取消的方式就是寻找在样本点个数固定的情况下最大的H(x1, x2, …, xN)取值，公式如5-2所示。
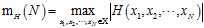(公式5-2）
符号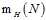
表示一个比无限大的M小且与假设空间H有关的关于样本大小N的函数。这一函数叫做成长函数（growth function）。
如何具体化（就是只使用训练样本的大小N来表达出该函数）成长函数成为接下来需要解决的问题。先从简单的例子着手一步一步的推导到在感知器下该函数的具体表达。
第一个例子是举一个最简单的情况，在一维实数的情况下，并且限制分类的正方向指向固定的一边，求解成长函数。给这一分类情况起名叫做正射线（positive rays），如图5-8所示。
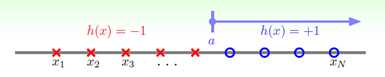
图5-8 正射线的二元分类
用数学的方式表示如下：
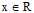，R为实数集；
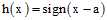，其中a是阈值，表示大于某个实数a数据被分为正类，反之为负类。正射线分类的成长函数很容易得出，如公式5-3所示。
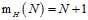（公式5-3）
求出的思路很简单， N个点两两之间的空隙个数为N-1，再加上端点的个数2（左端点是全正，右端点是全负），且可得出在N很大的情况下公式5-4成立。
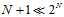（公式5-4）
课后题中提到了不规定正方向的情况下成长函数的计算即求在一维情况下感知器的分类情况，如公式5-5所示。
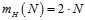（公式5-5）
求解的思路为，在N个点上两两之间有2·(N-1)中可能，因为正方向没有规定了，所以此处比正射线的种类多出了一倍，剩下样本点都为正类，或者都为负，这两种情形，因此再加上一个2。
下一个例子还是在一维空间里，与正射线分类不同的是，这是一种中间为正两边为负的情况，叫做中间为正的分类（positive interval），如图5-9所示。
图5-9 中间为正的分类
其成长函数不难求出，如公式5-6所示。
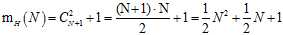(公式5-6）
求解思路如下：此为一个两端都不固定范围的分类（正射线是固定一个端点，直接到头都为一种类型），因此在N+1个空隙中选择两个作为端点（样本两两之间有N-1个空隙，两端还各有一个），因此为一个组合问题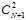
，但是少算了一种全负情况，即两个端点在同一个空隙之中（是哪个空隙不重要，只要落到一起即为全负），所以再加1。
同样在N很大时，也小于上限，如公式5-7所示。
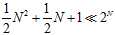（公式5-7）
接着举一个二维平面上的例子，以凸图形分类为例，在凸区域内部为正，外部为负，也就是凸区域的边界作为假设函数的划分线，如图5-10所示。
图5-10 a) 蓝色部分表示一种凸的图形 b）蓝色部分表示非凸的图形
如何求解在这种情形下的成长函数？成长函数是寻找一个最大值的情形，因此要取一些极端的情况，比如所有的点都落在一个圆圈上，用一个凸多边形将所有正类的样本点连接起来，将此图形稍微的放大一点，得到的凸多边形，其中间的区域为正，外边的区域为负，如图5-11所示。
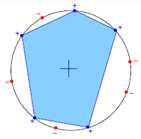
图5-11 凸多边形分类
课程里说到此处就直接给出结果了，如公式5-8所示。
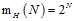（公式5-8）
看了很久不知道为啥，想了两种可能的解释，不知道是否正确，
一种是将这个圆圈想象成一条直线，在这条直线上每个样本点不是根据一个端点或者两个端点来确定它的正类的范围，而是每个样本都可以为正类，即使它们不相邻，于是解释就简单了，每个点都可以选择为正类或者负类，就是每个点都有两种可能的情况，那么N个点就可能有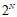
种情况。
另外一种想法是直接在二维平面上画图，在这里就阐述一下，以五个样本作为例子，如图5-12所示。
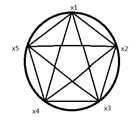
图5-12 五个样本点的凸多边形分类
将这五个样本点分成两类的方法一共有多少种（和正射线分类一样，正方向是有限制的，即多边形内部为正），从最简单两种情况出发，全为正和全为负，其相加为2，然后是四个样本为正的情况有多少种（就是图中有多少个凸四边形），就是从五个样本中取4个的情况有几种，答案是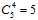
，然后是有多少个三角形，就是图中三个样本为正的情况，答案是
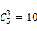，接着是有多少个直线，将样本点画成2个样本为正的情况，答案是
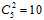，最后是只有一个样本点为正的情况，答案是
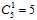，将所有的情况加起来得
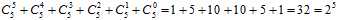，推广到N中情形，如公式5-9所示。
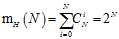（公式5-9）
以上公式可以通过二项式推导出来，不是凑巧左边的形式正好等于2的N次方的形式，二项式的推导如公式5-10所示。
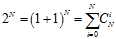（公式5-10）
如果N个样本点可以写出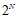
种类型的假设，即公式5-8成立的情况下，我们称N个样本点满足完全二分类情形（shattered），即可以分为
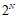种二分类（dichotomy）。
突破点。
将上一节中列举出来的所有成长函数列在表5-3中。
表5-3 各分类的成长函数
|
正射线 |
|
|
一维空间的感知器 |
|
|
间隔为正的分类 |
|
|
凸图形分类 |
|
|
二维平面的感知器 |
|
更希望得到一种多项式（polynomial）形式的成长函数，而不是指数（exponential）形式的，因为这样上界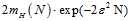
的下降速度将会更快。能否找出一种规律将表中二维感知器的成长函数也写成多项式形式的呢？于是提出了一个新的概念，突破点（break point）。
那什么叫突破点呢？对于三个样本点的感知器，所有的样本还是满足完全二分类情形（shattered，也就是还是可以最大化分类的），但是四个样本是却不能满足完全分类情形（不能满足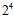
种分类了），于是我们称不能满足完全分类情形的样本数量为突破点，可以想象得出当有更多的样本点时，一定也不能满足完全分类情形。因此二维感知器成长函数的突破点是4。在通过一个表5-4来说明上节提到的所有分类情况。
表5-4各分类的突破点与成长函数的关系
|
正射线 |
突破点是2 |
|
|
一维空间的感知器 |
突破点是3 |
|
|
间隔为正的分类 |
突破点是3 |
|
|
凸图形分类 |
没有 |
|
|
二维平面的感知器 |
突破点是4 |
|
从表中可以看出可能成长函数和突破点之间有一定的关系，即突破点是k的情况下，成长函数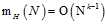
。（但是这是一个过于宽松的上界，从表5-4的第二行可以看出成长函数实际比这个规律要小）
标签：
原文地址：http://www.cnblogs.com/ymingjingr/p/4285358.html
接近0的假设。
接近0的假设的几率变大。
在某些情况
在某些情况